
نیکولو ماکیاولی (Niccolò Machiavelli) سیاستمدار و فیلسوف ایتالیایی دوران رنسانس در کتاب خود شهریار (The Prince) خطاب به شاهزادگان (مدیران دوران رنسانس) توصیه میکند وقتی مشکلی در مملکتتان رخ میدهد، بخصوص آنهایی که ممکن است شما را بهشدت وحشتزده کند، بلافاصله واکنش نشان ندهید، بهترین سیاست این است که در تصمیمگیری خود تأخیر بیندازید. او میگوید تقریباً همیشه آنهایی که بلافاصله به مشکلات واکنش نشان میدهند حجم مشکلات را بزرگتر میکنند و آن را سرعت میبخشند و همان چیزی که از آن وحشت داشتند بر سرشان خراب میشود.
در این مورد، مقاله “نردبان استنتاج: چرا ما بهسرعت نتیجهگیری میکنیم؟” نکات جالبی را بحث میکند.
واکنش بیشازاندازه (Overreaction) که ماکیاولی شهریاران را از آن حذر میکند، گریبانگیر مدیران امروز نیز هست. یکی از دلایل بروز چنین پدیدهای عدم درک مدیران از مفهوم واریانس (Variance) در فرآیندهای کسبوکار است.
واریانس چیست؟
واریانس یک مفهوم آماری است که نشان میدهد مقادیر یک متغیر تصادفی چگونه حول میانگین آن توزیع شدهاند. فرض کنید وزن حقیقی شما ۷۵ کیلوگرم است. شما دو ترازو دارید که وزن خود را با آن اندازهگیری میکنید. مانند هر وسیله اندازهگیری، این دو دقیق نیستند و دارای کمی خطا هستند. فرض کنید روی هر ترازو ۱۰۰ بار وزن خود را اندازهگیری و مقادیر آن را ثبت میکنید. من این مسئله فرضی را در کامپیوتر شبیهسازی کردم و نمودار توزیع دو ترازو را در شکل-۱ رسم کردم. این نمودار نشان میدهد برای مثال در ۱۵ بار از ۱۰۰ بار وزنکشی، ترازوی الف وزن شما را ۷۴٫۵ کیلوگرم نشان داده است.
وقتی میانگین اعداد بهدستآمده از هر دو ترازو را مقایسه میکنیم، هر دو میانگینی نزدیک ۷۵ کیلوگرم دارند. بااینوجود ترازوی الف با فرکانس بیشتری وزن شما را نزدیک به وزن اصلی شما یعنی ۷۵ کیلوگرم نشان میدهد. درحالیکه ترازوی ب اعداد متنوعتری را به شما نشان میدهد. بهعبارتدیگر، اعدادی که ترازوی ب نشان میدهد پراکندگی بیشتری حول میانگین دارند.
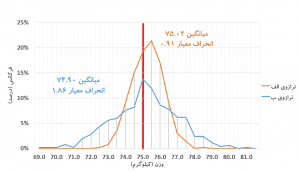
در عمل شما وزن حقیقی خود را نمیدانید و ترازو قرار است وزن شما را مشخص کند. همینطور شما برای سنجش وزن خود تنها یک یا حداکثر چند بار روی ترازو میروید. در این حالت ترازوی الف با احتمال بیشتری وزن شما را نزدیک به وزن حقیقیتان نشان خواهد داد. در مقابل وزنکشی با ترازوی ب با عدم قطعیت بیشتری همراه است.
پراکندگی دادهها حول میانگین را میتوان با انحراف معیار (Standard Deviation) سنجید. همانطور که در شکل-۱ مشخص است انحراف معیار ترازوی ب تقریباً دو برابر ترازوی الف است.
برای آشنایی با تعریف ریاضی واریانس و انحراف معیار مقاله “شاخصهای پراکندگی در آمار” را بخوانید.
انحراف معیار یکی از شاخصهایی است که با آن میتوان عدم قطعیت در سیستمها را به شکل کمّی سنجش کرد.
اثر ارائه پیوسته اطلاعات بر درک سرمایهگذار از عملکرد سهام در بازارهای مالی
فرض کنید فردی در سهام یک شرکت در بورس سرمایهگذاری میکند. این سهام بهطور میانگین دارای نرخ بازده سالیانه ۱۵ درصد با انحراف معیار ۱۰ درصد است. معنی دیگر جمله این است که در ۶۸ درصد موارد بازده سالیانه این سهام بین ۵ درصد تا ۲۵ درصد است. همینطور به این معنی است که او در ۹۳ درصد مواقع، در انتهای هرسال سود خواهد کرد و بازده بزرگتر از صفر به دست میآورد (توضیحات در بخش ضمیمه مقاله آمده است).
سرمایهگذاری ایمن و خوبی به نظر میرسد. باوجود عدم قطعیت ۱۰ درصدی، با احتمال زیادی او در انتهای سال خوشحال خواهد بود. حال فرض کنید همین سهام را در بازه زمانی کوتاهتری برای مثال هر سه ماه یکبار تحلیل کنیم. با محاسباتی که در بخش ضمیمه این مقاله آوردم نشان دادم که او در پایان هر سه ماه در ۷۷ درصد مواقع سود خواهد کرد. اگر همینطور بازههای زمانی را کوچکتر و کوچکتر کنیم احتمال آنکه در پایان هرماه روی این سهام سود کند به ۶۷ درصد و در پایان هرروز ۵۴ درصد میشود (شکل-۲).
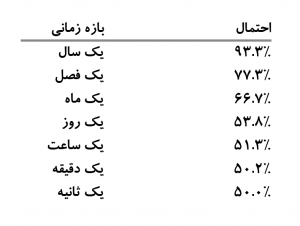
مانند مثال ترازو، او بهعنوان سرمایهگذار از بازده واقعی سهام و توزیع آن خبر ندارد. آنچه او میبیند تغییرات ساعتی و روزانه قیمت سهام است. برای این سهام، او تنها کمی بیش از ۵۰ درصد شانس دارد که در پایان هرروز ضرر نکند. در این حالت هرروز با منفی شدن قیمت، او احساس ناراحتی میکند. با مثبت شدن قیمت کمی احساس بهتری میکند اما تئوری چشمانداز احتمالی (Prospect Theory) توضیح میدهد که خوشحالی او بهاندازهای نیست که ناراحتی معادل قبلی او را جبران کند. تئوری چشمانداز احتمالی بیان میکند که انسانها در هنگام ضرر کردن، مطلوبیتی که از دست میدهند تقریباً دو برابر مطلوبیت زمانی است که سود معادل آن را به دست میآورند. به این شکل قابلفهم است که او در نهایت ازنظر روانی و احساسی فرسوده خواهد شد.
نکته مهم دیگر این است که سرمایهگذاری که هرروز قیمت سهامش را بررسی میکند تصویر کاملاً متفاوتی از سودآوری آن به دست میآورد. سهامی که در پایان سال یک سرمایهگذاری موفق بود وقتی در بازههای زمانی روزانه بررسی میشود یک سرمایهگذاری ناموفق است.
این مسئله به مفهوم مقیاس در فرآیندهای تصادفی (Scaling Property of Randomness) برمیگردد. درواقع چون فرآیند دارای واریانس است، آنچه سرمایهگذار از بالا پایین رفتنهای قیمت در بازههای زمانی کوچک میبیند بیشتر ناشی از تصادف است تا نشاندهنده یک تغییر بنیادی.
نویز در مقابل اطلاعات
ممکن است برخی مواقع که با تلفن صحبت میکنید صداهای پسزمینه نامطلوبی به گوشتان برسد، این صداها نویز (Noise) هستند. آنچه برای شما اهمیت دارد صدای طرف مقابل است؛ اما نویز بر روی کیفیت صدای دریافتی اثر میگذارد. در مهندسی نسبت سیگنال به نویز (Signal-to-Noise: SNR) نشان میدهد میزان سیگنال مطلوب به نویز پسزمینه چقدر است. حالت مناسب این است که نسبت سیگنال به نویز بیشینه شود.
از منظر دیگر در مثال پیشین، اطلاعات مربوط به قیمت که سرمایهگذار در هرروز دریافت میکند بیشتر نویز هستند تا اینکه اطلاعات باارزشی باشند. اگر بخواهم به شکل کمّی این موضوع را تبیین کنم، در حالتی که سرمایهگذار اطلاعات را سالیانه بررسی میکند نسبت سیگنال به نویز ۱٫۵ است. وقتی او ماهیانه تغییرات قیمتی همان سهام را مشاهده میکند نسبت سیگنال به نویز ۰٫۴۳ میشود. برای مشاهدات ساعتی این نسبت نزدیک ۳ درصد است؛ یعنی او به ازای هر واحد اطلاعات باارزشی که دریافت میکند، ۳۰ واحد نویز میگیرد (توضیحات در بخش ضمیمه مقاله آمده است).
جمعبندی آنکه وقتی سرمایهگذار در بازههای زمانی کوتاهتری عملکرد سهام را بررسی میکند احتمال آنکه ناراضی شود بالاتر میرود. این نارضایتی ممکن است موجب شود او سهامی را که ممکن است در بازه یکساله خوب عمل کند، بفروش برساند. در این حالت سرمایهگذار صرفاً روی تغییرات کوچک توجه خود را متمرکز کرده و قادر به دیدن روند کلی نیست.
زنجیره تأمین و اثر شلاقی
بسیاری از متغیرهای کسبوکار مانند تقاضا، بازده سهام، نرخ خروج کارکنان، نرخ خرابی ماشینآلات تحت تأثیر فرآیندهای تصادفی هستند. تقاضای یک محصول در یک بازه زمانی معمولاً از یک روند کلی پیروی میکند ولی در هر دوره (برای مثال هرماه) میزان تقاضا حول آن روند به شکل تصادفی توزیع میشود (شکل-۳).
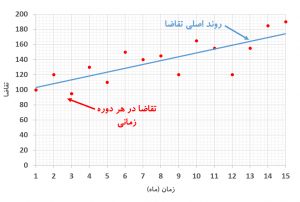
خردهفروشی را تصور کنید که در یک ماه با تقاضایی بالاتر از معمول مواجه میشود. خردهفروش باید چگونه به این مسئله پاسخ دهد؟ یک توضیح آن است که این نوسان تنها به علت تصادف به وجود آمده است. در این حالت او تغییری در سطح انبار به وجود نخواهد آورد. ولی اگر او این افزایش تقاضا را سیگنالی مبنی بر تغییر بنیادی تقاضا درک کند بهمنظور پوشش تقاضاهای آتی بلافاصله شروع به پر کردن انبار خود میکند. این واکنش ناگهانی خردهفروش منجر به بروز اثر شلاقی (Bullwhip Effect) در طول زنجیره تأمین میشود.
فرض کنید این افزایش ناگهانی تقاضا تصادفی بوده باشد و تغییر بنیادی در تقاضا ایجاد نشده اما خردهفروش آن را دلالت بر تغییر روند گرفته است. بنابراین خردهفروش شروع به سفارش بیشازحد محصول میکند. در دوره زمانی بعد که تقاضا به حالت عادی برمیگردد، انبار او بیشازحد از محصول پرشده و او میزان سفارش را بهاندازهای کاهش میدهد تا انبارش را خالی کند. به علت سفارش بیشازحد نیاز و کمتر از حد نیاز واریانس سفارش دهی خردهفروش بیش از واریانس تقاضا میشود.
گرچه منطقی به نظر میرسد که با مشاهده افزایش ناگهانی تقاضا، سفارش کالا را بیشتر کنیم، اما انسانها معمولاً واکنش بیشازحد از خود نشان میدهند. برای مثال اگر تقاضا ۱۲۵ درصد افزایشیافته، خردهفروش با خود فکر میکند در جهت اطمینان بهتر است ۱۵۰ درصد سفارش خود را افزایش دهد. مشابه خردهفروش، عمدهفروش تقاضای بیشازاندازه او را میبیند و او هم واکنش بیشازاندازه از خود نشان میدهد. این اثر با شدت بیشتر در طول زنجیره تأمین پیش میرود و آشفتگی را منتشر میکند.
اثر شلاقی زمانی پیش میآید که نوسان جزئی در تقاضا با شدت زیاد به سمت بالادست زنجیره تأمین حرکت کند. این اثر بهویژه درزمانی که عناصر زنجیره تأمین تنها اطلاعات تقاضای عنصر قبل از خود را داشته باشند، شدت میبخشد (شکل-۴). شاید دیده باشید که محصولی در یک دوره زمانی ناگهان نایاب و در یک دوره زمانی دیگر بهوفور در بازار دیده میشود ولی تقاضایی برای آن وجود ندارد. یکی از دلایل این امر وجود اثر شلاقی در زنجیره تأمین است.
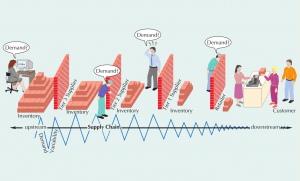
پیام این بحث برای مدیران چیست؟
در دنیای امروز ما بهطور پیوسته در معرض انواع اطلاعات هستیم. این اطلاعات ما را به این سمت سوق میدهند که واکنش نشان دهیم. اما همانطور که ماکیاولی شهریاران را اندرز میدهد، واکنشهای لحظهای به اتفاقات در دنیای کسبوکار اغلب وضع را بدتر میکند. مدیران باید آگاه باشند بیشتر اطلاعات لحظهای که دریافت میکنند همراه با نویز است. آنان بهجای توجه به اطلاعات بیفایده باید روندها را تشخیص دهند. شاید به همین خاطر است برخی توصیه میکنند بهجای خواندن اخبار اقتصادی روزانه که نویز زیادی دارد، بهتر است مجلات اقتصادی هفتگی را بخوانید.
اگر به موضوعات مطرحشده در این مقاله علاقمند شدید توصیه میشود مقاله “خطا در استفاده از میانگین” را مرور کنید.
***ضمیمه: محاسبات
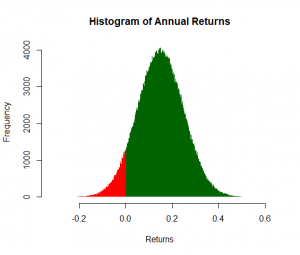
میتوان فرض کرد بازده سهام اشارهشده در مقاله، از توزیع نرمال (با میانگین ۱۵ درصد و انحراف معیار ۱۰ درصد) پیروی میکند. در این صورت برای محاسبه احتمال سودآور بودن سهام کافی است محاسبه کنیم با چه احتمالی بازده سهام از صفر بزرگتر است (). برای این منظور کد زیر را در R اجرا کردم. نمودار شکل-۵ توزیع بازده سالیانه سهام را برای یکمیلیون بار شبیهسازی نشان میدهد. بخش سبزرنگ نشان میدهد چند بار از اینیک میلیون بار، بازده سهام مثبت بوده است.
1 2 3 4 5 6 7 8 9 10 11 12 | > #15% return > Mean <- 0.15 > # 10% error rate per annum > Sigma <- 0.10 > #P(X>0) > pnorm(0, mean = Mean, sd = Sigma, lower.tail = F) [1] 0.9331928 > #Graph > Returns <- rnorm(n = 10^6, mean = Mean, sd = Sigma) > H <- hist(Returns, breaks = 1000, plot = F) > cuts <- cut(H$breaks, c(-Inf, 0, Inf)) > plot(H, col = c("red", "dark green")[cuts], lty = "blank", main = "Histogram of Annual Returns") |
وقتی بازههای مشاهده () کوچکتر میشود روابط زیر برای محاسبه میانگین (
) و انحراف معیار (
) بازده سهام بر اساس مقادیر متناظر سالیانه آنها استفاده میشوند:
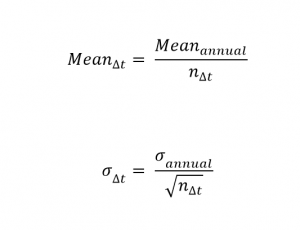
در رابطه بالا برابر با تعداد بازههای زمانی موردنظر در یک سال است. برای مثال در حالت فصلی، این مقدار ۴ است.
برای محاسبه نویز در بازههای زمانی مختلف، یکی از تعاریفی که در مهندسی برای نسبت سیگنال به نویز استفاده میشود نسبت میانگین سیگنال () به انحراف معیار نویز (
) است.
کد زیر را در R برای محاسبه مقادیر بهدستآمده در شکل-۱ و مقادیر نویز استفاده کردم. ضمناً فرض شده است بازار سهام ۲۵۲ روز فعال و هرروز ۸ ساعت کاری است.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | > Time <- c(1, 4, 12, 252, 252 * 8, 252 * 8 * 60, 252 * 8 * 60 * 60) > label <- c("Year", "Quarter", "Month", "Day", "Hour", "Minute", "Second") > # P(X>0) & SNR > Table <- data.frame(N_Delta_T = Time, + Probability <- round(pnorm(0, mean = Mean / Time, sd = Sigma / sqrt(Time), lower.tail = FALSE), 3) , + SNR = round((Mean / Time) / (Sigma / sqrt(Time)), 3), row.names = label) > Table N_Delta_T Probability SNR Year 1 0.933 1.500 Quarter 4 0.773 0.750 Month 12 0.667 0.433 Day 252 0.538 0.094 Hour 2016 0.513 0.033 Minute 120960 0.502 0.004 Second 7257600 0.500 0.001 |
منابع:
Bushberg, J. T. (Ed.). (2002). “The Essential Physics of Medical Imaging”, Lippincott Williams & Wilkins
Cachon, G., & Terwiesch, C. (2009). “Matching Supply with Demand: An introduction to Operations Management”, Irwin Professional Pub
Finch, N., Ford, G., Cuganesan, S., & Carlin, T. M. (2005). “The Scaling Property of Randomness: The Impact of Reporting Frequency on the Perceived Performance of Investment Funds”, White Paper
Russell, R. S., & Taylor-III, B. W. (2008). “Operations Management along the Supply Chain”, John Wiley & Sons
Sterman, J. D. J. D. (2000). “Business Dynamics: Systems Thinking and Modeling for a Complex World”, Irwin/McGraw-Hill
Taleb, N. (2005). “Fooled by Randomness: The Hidden Role of Chance in Life and in the Markets”, Random House Incorporated

سلام
از این خواندن این مقاله لذت بردم.
به خصوص اینکه کد هم داشت! 🙂
بسیار عالی بود
داشتن کد داخل مقاله یک مزیت فوقالعادست.
سپاس
واقعا عالی و جامع بود. لذت بردم
بابا تو دیگه کی هستی?
ممنون. بسیار خوب بود
بسیار عالی بود
خدا خیرتون بده ، خیلی مفید بود . در مورد این مطلب منابع یا کتابی نیز می توانید معرفی نمایید ؟
با سلام،
از بازخوردتان متشکرم. لطفا به بخش منابع همین مقاله که در انتها آمده است، مراجعه کنید. بطور مشخص کتابهای نسیم طالب را در این حوزه توصیه میکنم.
موفق باشید.
در صورتی که نوسان بجای سمت تقاضا در سمت عرضه وجود داشته باشد چطور می توان اثر شلاقی را خنثی کرد؟
برای مثال عرضه گوجه در مقاطعی از سال کم می شود و قیمت آن به شدت رشد می کند و در زمان هایی نیز عرضه از تقاضا پیشی می گیرد و قیمت بسیار نازل می شود. در این موارد و مشابه به این که عرضه تاثیر گذار بر فرایند است چگونه رفتار می شود؟
سپاسگزارم از مقاله کاربردیتون
از خواندن مقاله خیلی لذت بردم
واقعا لذت بردم ممنونم
بسیار ساده و کاربردی توضیح داده شده بود . ممنون
عالی و کاربردی بود. ممنونم
من همیشه ریاضی ام ضعیف بود چون هیچ معلمی نمیگفت اینها کجای زندگی به کار میاد و مفهومشون چیه