مروری بر تبدیل Box-Cox و کاربردهای آن

بسیاری از تحلیل‌های آماری و پاره‌ای از الگوریتم‌های یادگیری ماشین مبتنی بر این فرض است که نمونه از جامعه‌ای با توزیع نرمال (Normal Distribution) به دست آمده و ساختار خطا جمعی است (Additive Error Structure). جمعی بودن ساختار خطا به این معنی است که خطا تنها به مقدار واقعی اضافه می‌شود و خودش وابسته به آن مقدار واقعی نیست.

زمانی که این مفروضات برقرار نباشد، بسته به اینکه تا چه میزان مدل به نقض این مفروضات حساس است و تا چه حد این مفروضات نقض شده عملکرد مدل تحت تأثیر قرار می‌گیرد. اگر این مفروضات نقض شود، چند راهکار وجود دارد:

درصورتی‌که میزان انحراف از مفروضات کم است، تحلیل را با مدل ادامه دهیم.

از مدل‌هایی برای تحلیل استفاده کنیم که نیاز به این مفروضات ندارد.

داده‌ها را به شکلی تبدیل کنیم که این مفروضات برقرار شوند.

بحث من در این مقاله درباره رویکرد سوم است. تبدیل Box-Cox سعی دارد داده‌ها را به‌گونه‌ای تغییر دهد به امید آنکه داده‌های تغییریافته به توزیع نرمال نزدیک‌تر شوند. به‌این‌ترتیب روش‌‌های آماری که نیاز به این فرض دارند، روی داده تبدیل‌یافته اعمال شود.

تبدیل Box-Cox

اگر $x$ متغیر اصلی باشد، تبدیل Box-Cox آن ( $\tilde{x}$ ) از رابطه زیر محاسبه می‌گردد:

$\tilde{x} = \left\{\begin{matrix} (x^{\lambda } - 1) / \lambda, \: if \: \lambda \neq 0 \\ log(x) , \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: if \: \lambda = 0 \end{matrix}\right.$

در رابطه بالا، لاندا ( $\lambda$ ) پارامتری است که باید برآورد شود تا بتوان تغییر متغیر را انجام داد. برای تعیین لاندا، باید مقادیر مختلفی آزمایش شود و لاندای بهینه که از بین همه این مقادیر، توزیع $\tilde{x}$ را به نرمال نزدیک‌تر می‌کند، انتخاب گردد. معمولاً مقادیر محتمل لاندا در بازه ۶- تا ۶ بر اساس الگوریتم برآورد بیشینه درستنمایی (Maximum Likelihood Estimation – MLE) بررسی و مقدار بهینه انتخاب می‌شود. به زبان ساده، الگوریتم برآورد بیشینه درستنمایی به دنبال لاندایی است که متغیر x را به‌گونه‌ای تغییر دهد که توزیع متغیر تبدیل‌یافته $\tilde{x}$ تا جای ممکن به توزیع نرمال نزدیک شود.

در عمل طی یک فرآیند تکرارشونده، لاندایی پیدا می‌شود که منفی لگاریتم تابع درستنمایی (Minus Logarithm of the Likelihood Function) را بیشینه می‌کند. خروجی این فرآیند برآورد نقطه‌ای (Point Estimate) از لاندا و برآورد بازه‌ای (Interval Estimate) آن است. دقت کنید، اگر صفر در برآورد بازه‌ای قرار گرفت، آنگاه نمی‌توانیم بگوییم که لاندا تفاوت معنی‌داری با صفر دارد، پس آن را مساوی صفر قرار می‌دهیم.

توجه کنید که هیچ تضمینی نیست که همیشه تغییر متغیر پیشنهادی الگوریتم Box-Cox منجر به نرمال شدن داده شود. اگر میزان چولگی داده‌ها بسیار زیاد باشد، ممکن است از دست این روش هم کاری برنیاید. بنابراین همیشه بهتر است بررسی کنید آیا متغیر تبدیل‌یافته از توزیع نرمال پیروی می‌کند یا خیر.

پیاده‌سازی تبدیل Box-Cox در R

برای آنکه من نحوه اجرای تغییر متغیر را نشان دهم، در زبان R هزار عدد تصادفی از توزیع گاما (Gamma Distribution) با پارامترهای shape = 1 و rate = 1 ایجاد کردم و آن را در بردار x ذخیره کردم. شما می‌توانید هر داده دیگری را به‌جای $x$ بکار ببرید.

#Create a sample data
set.seed(1234) 
x <- rgamma(1000, shape = 1, rate = 1)

#Create a sample data

set.seed(1234)

x <- rgamma(1000, shape = 1, rate = 1)

من در مقاله “بررسی نرمال بودن داده‌ها” توضیح دادم چگونه ارزیابی کنید که آیا یک نمونه داده از توزیع نرمال به دست آمده است. دو روش ساده که می‌توان استفاده کرد رسم هیستوگرام و نمودار چندک-چندک (Q-Q Plot) است. گرچه در آن مقاله من استفاده از آزمون‌های آماری را هم توصیه کردم، برای سادگی در اینجا به همین دو روش اکتفا می‌کنم.

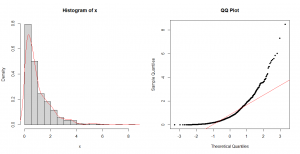
در شکل-۱، داده‌های بردار x را در قالب هیستوگرام نمایش دادم و تابع توزیع برآوردی را با منحنی قرمزرنگ روی هیستوگرام انداختم. مشخص است که داده‌ها چولگی زیادی به سمت راست دارند. نمودار چندک-چندک و مقایسه آن با خط ۴۵ درجه هم نشان می‌دهد که داده‌ها از توزیع نرمال پیروی نمی‌کنند.

#Histogram
par(mfrow = c(1, 2))
hist(x, probability = T, breaks = 15) 
lines(density(x), col = "red", lwd = 2)

#QQ-plot 
qqnorm(x, main = "QQ Plot", pch = 20) 
qqline(x, col = "red", lwd = 2)

#Histogram

par(mfrow = c(1, 2))

hist(x, probability = T, breaks = 15)

lines(density(x), col = "red", lwd = 2)

#QQ-plot

qqnorm(x, main = "QQ Plot", pch = 20)

qqline(x, col = "red", lwd = 2)

سپس در کد زیر از تبدیل Box-Cox استفاده کردم تا داده‌ها را به توزیع نرمال نزدیک کنم. برای اجرای الگوریتم در R از کتابخانه MASS بهره بردم. این کتابخانه تابعی به نام boxcox دارد. آرگومان اولی که به تابع دادم نشان می‌دهد قرار است تغییر متغیر را برای x بکار ببرم. در آرگومان دوم مقادیر محتمل لاندا را در قالب یک بردار که درایه‌های آن از ۶- تا ۶ است و با یکدیگر به‌اندازه ۰٫۱ فاصله دارند، وارد کردم. نتایج الگوریتم را در res ذخیره کردم و آن را به دیتا فریم تبدیل کردم. پنج سطر اول این دیتا فریم در زیر آمده است. ستون x همان مقادیر محتمل لاندا هستند و ستون y مقادیر منفی لگاریتم تابع درستنمایی هستند.

#Required library
library('MASS')

#Box-Cox transformation
par(mfrow = c(1, 1))
res <- boxcox(x ~ 1, lambda = seq(-6, 6, 1 / 10))

res <- as.data.frame(res)
head(res, 5)
    x         y
1 -6.0 -232.3445
2 -5.9 -228.1366
3 -5.8 -223.9359
4 -5.7 -219.7425
5 -5.6 -215.5568


#Find the best lamda
best_lamda <- res[which.max(res$y), 'x']
best_lamda
0.6

#Required library

library('MASS')

#Box-Cox transformation

par(mfrow = c(1, 1))

res <- boxcox(x ~ 1, lambda = seq(-6, 6, 1 / 10))

res <- as.data.frame(res)

head(res, 5)

x y

1 -6.0 -232.3445

2 -5.9 -228.1366

3 -5.8 -223.9359

4 -5.7 -219.7425

5 -5.6 -215.5568

#Find the best lamda

best_lamda <- res[which.max(res$y), 'x']

best_lamda

0.6

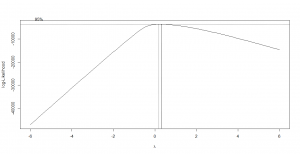
وقتی الگوریتم اجرا می‌شود، نموداری هم بلافاصله رسم می‌شود که در شکل-۲ آوردم. محور افقی این نمودار، مقادیر لاندا و محور عمودی آن منفی لگاریتم تابع درستنمایی است. همان‌طور که در شکل مشخص است با نقطه‌چین برآورد بازه‌ای ۹۵ درصد اطمینان برای لاندا هم آمده است. توجه کنید که آیا مبدأ مختصات (صفر) در این بازه قرار گرفته یا نه. در این مثال مشخص است که صفر در این بازه نیست، بنابراین لاندا با صفر تفاوت معنی‌داری دارد و مقدار برآورد نقطه‌ای (۰٫۶) را می‌پذیرم.

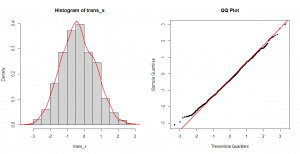
در گام بعد طبق فرمول پیشنهادی، تغییر متغیر را انجام دادم و آن را در trans_x ذخیره کردم. بررسی هیستوگرام و نمودار چندک-چندک trans_x نشان می‌دهد، توزیع آن بسیار به توزیع نرمال نزدیک شده است.

مثالی از کاربرد تبدیل Box-Cox در محاسبه ضریب همبستگی

در این مثال، به دنبال آن هستم که ضریب همبستگی بین دو متغیر را که یکی از آنان به‌شدت چولگی دارد، محاسبه کنم. فرض کنید x و y دو متغیر هستند که از هرکدام یک نمونه ۲۵تایی جمع‌آوری کردم:

#Create sample data
x <- c(33, 31, 46, 21, 3,
       18, 15, 19, 12, 8,
       25, 18, 17, 10, 19,
       31, 14, 25, 14, 27,
       43, 24, 19, 23, 27)

y <- c(0.06, 0.05, 0.01, 0.13, 1.98,
       0.13, 0.1, 0.11, 0.14, 0.51,
       0.03, 0.07, 0.14, 0.58, 0.03,
       0.06, 1.3, 0.03, 0.35, 0.31,
       0.02, 0.08, 0.33, 0.04, 0.03)

#Create sample data

x <- c(33, 31, 46, 21, 3,

18, 15, 19, 12, 8,

25, 18, 17, 10, 19,

31, 14, 25, 14, 27,

43, 24, 19, 23, 27)

y <- c(0.06, 0.05, 0.01, 0.13, 1.98,

0.13, 0.1, 0.11, 0.14, 0.51,

0.03, 0.07, 0.14, 0.58, 0.03,

0.06, 1.3, 0.03, 0.35, 0.31,

0.02, 0.08, 0.33, 0.04, 0.03)

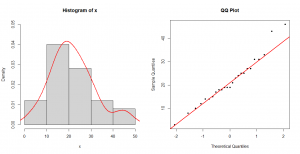
توزیع این متغیرها به همراه نمودار چندک-چندک در شکل-۴ و شکل-۵ آمده است. همان‌طور که مشاهده می‌شود x انحراف چندانی از توزیع نرمال ندارد ولی y چولگی به سمت راست دارد.

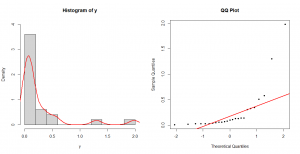
سپس ضریب همبستگی پیرسون را برای x و y محاسبه کردم و آزمون فرضیه متناسب را برای آن انجام دادم. همبستگی پیرسون (Pearson Correlation Coefficient) بین این دو متغیر ۰٫۵۸ – به دست می‌آید و آزمون فرضیه آن نیز معنی‌دار می‌شود (به این معنی که ضریب همبستگی پیرسون با صفر تفاوت معنی‌داری دارد). توجه کنید که یکی از مفروضات آزمون فرضیه برای ضریب همبستگی نرمال بودن متغیرها است.

#Pearson correlation
cor(x, y, method = "pearson")
-0.5818021

cor.test(x, y, method = "pearson")

	Pearson's product-moment correlation

data:  x and y
t = -3.4306, df = 23, p-value = 0.002283
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.7943268 -0.2423949
sample estimates:
       cor 
-0.5818021

#Pearson correlation

cor(x, y, method = "pearson")

-0.5818021

cor.test(x, y, method = "pearson")

Pearson's product-moment correlation

data: x and y

t = -3.4306, df = 23, p-value = 0.002283

alternative hypothesis: true correlation is not equal to 0

95 percent confidence interval:

-0.7943268 -0.2423949

sample estimates:

cor

-0.5818021

شکل-۶ نمودار پراکندگی به همراه خط برآوردی رگرسیون y روی x را نشان می‌دهد.

#Scatterplot
plot(x, y)
#Add regression line
abline(lm(y ~ x), col = 'red', lwd = 3)

#Scatterplot

plot(x, y)

#Add regression line

abline(lm(y ~ x), col = 'red', lwd = 3)

می‌دانیم توزیع متغیر y با توزیع نرمال تفاوت فاحشی دارد. پس بهتر است راهکارهای دیگری را هم بررسی کنیم.

یک راهکار این است که از روشی مانند ضریب همبستگی اسپیرمن (Spearman Correlation Coefficient) استفاده کنیم که نیاز به فرض نرمال بودن ندارد. در کد زیر ضریب همبستگی اسپیرمن به همراه آزمون فرضیه مربوطه را پیاده‌سازی کردم. این آزمون‌ نیز نتایج مشابهی دارد و فرضیه صفر را رد می‌کند. ولی توجه کنید که ضریب همبستگی اسپیرمن ۰٫۷۹ – است بدان معنی که شدت رابطه خطی را بیشتر از ضریب پیرسون برآورد می‌کند.

#Spearman correlation
cor(x, y, method = "spearman")
-0.7935499

cor.test(x, y, method = "spearman")
	Spearman's rank correlation rho

data:  x and y
S = 4663.2, p-value = 2.214e-06
alternative hypothesis: true rho is not equal to 0
sample estimates:
       rho 
-0.7935499

#Spearman correlation

cor(x, y, method = "spearman")

-0.7935499

cor.test(x, y, method = "spearman")

Spearman's rank correlation rho

data: x and y

S = 4663.2, p-value = 2.214e-06

alternative hypothesis: true rho is not equal to 0

sample estimates:

rho

-0.7935499

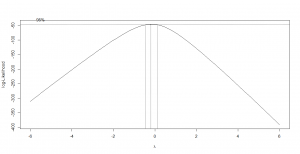
راهکار دیگر این است که توزیع متغیر y را با استفاده از رویکرد Box-Cox به توزیع نرمال نزدیک کنم. با روشی که در قبل توضیح دادم، الگوریتم Box-Cox را روی متغیر y پیاده‌سازی کردم. همان‌طور که از شکل-۷ مشخص است، پارامتر لاندا با صفر تفاوت معنی‌داری ندارد، بنابراین برآورد نقطه‌ای لاندا را معیار قرار نمی‌دهم و لاندا را مساوی صفر در نظر می‌گیرم. پس طبق پیشنهاد Box-Cox از تغییر متغیر لگاریتمی استفاده می‌کنم و متغیر تبدیل‌یافته را در trans_y ذخیره می‌کنم.

#Box-Cox transformation of y
res <- boxcox(y ~ 1, lambda = seq(-6, 6, 1/10))
res <- as.data.frame(res)

#Find the best lamda
best_lamda <- res[which.max(res$y), 'x']
best_lamda
-0.2

#Box-Cox transformation
trans_y <- log(y)

#Box-Cox transformation of y

res <- boxcox(y ~ 1, lambda = seq(-6, 6, 1/10))

res <- as.data.frame(res)

#Find the best lamda

best_lamda <- res[which.max(res$y), 'x']

best_lamda

-0.2

#Box-Cox transformation

trans_y <- log(y)

اگر ضریب همبستگی پیرسون بین x و trans_y و همچنین آزمون فرضیه برای ضریب همبستگی را محاسبه کنم، به نتایج زیر می‌رسم.

#Pearson correlation
cor(x, trans_y, method = 'pearson')
-0.7878329

cor.test(x, trans_y, method = 'pearson')

	Pearson's product-moment correlation

data:  x and trans_y
t = -6.1347, df = 23, p-value = 2.94e-06
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.9021326 -0.5702053
sample estimates:
       cor 
-0.7878329

#Pearson correlation

cor(x, trans_y, method = 'pearson')

-0.7878329

cor.test(x, trans_y, method = 'pearson')

Pearson's product-moment correlation

data: x and trans_y

t = -6.1347, df = 23, p-value = 2.94e-06

alternative hypothesis: true correlation is not equal to 0

95 percent confidence interval:

-0.9021326 -0.5702053

sample estimates:

cor

-0.7878329

ملاحظه می‌کنید در اینجا هم ضریب همبستگی ۰٫۷۹ – به دست می‌آید. یعنی در این حالت ضریب همبستگی پیرسون نسبت به زمانی که روی داده‌های خام محاسبه شد، ۲۷ درصد بهبود پیدا کرد. اگر نمودار پراکندگی بین x و trans_y را در شکل-۸ ملاحظه و با شکل-۶ مقایسه کنید، مشخص است که ابر داده‌ها به‌خوبی حول خط رگرسیون توزیع شده‌اند.

#Scatterplot
plot(x, trans_y)
#Add regression line
abline(lm(trans_y ~ x), col = 'red', lwd = 3)

#Scatterplot

plot(x, trans_y)

#Add regression line

abline(lm(trans_y ~ x), col = 'red', lwd = 3)

تبدیل Box-Cox برای رگرسیون خطی

همان‌طور که در مثال قبل مشاهده کردید، تغییر متغیر Box-Cox کیفیت رابطه خطی را بهبود داد. یکی از کاربردهای این رویکرد، در زمانی است که متغیر پاسخ (y) در رگرسیون خطی دارای چولگی بالاست.

تبدیل Box-Cox برای رگرسیون خطی به دنبال آن است که y را به‌گونه‌ای تغییر دهد که وقتی متغیر تبدیل‌یافته روی x برازش می‌شود، رابطه متغیر آن با x تا حد امکان به خط نزدیک شود. در این حالت نیز مشابه قبل به دنبال یافتن لاندای بهینه هستیم. در R می‌توانید با کدی مانند زیر الگوریتم Box-Cox را برای تغییر متغیر y در رگرسیون خطی روی x بکار ببرید:

boxcox(y ~ x, lambda = seq(-6, 6, 1 / 10))

1	boxcox(y ~ x, lambda = seq(-6, 6, 1 / 10))

نتیجه کد بالا مشابه قبل است و Box-Cox تغییر متغیر لگاریتمی را پیشنهاد می‌دهد.

توجه کنید گرچه رگرسیون خطی بالا تنها دارای یک متغیر پیش‌بینی کننده است، می‌توان از این رویکرد برای رگرسیون خطی چندمتغیره هم استفاده کرد.

***ضمیمه: پیاده‌سازی تبدیل Box-Cox در پایتون

در این بخش نحوه پیاده‌سازی الگوریتم را در پایتون نشان دادم. در ابتدا پس از فراخوانی کتابخانه‌ Numpy، هزار عدد تصادفی از توزیع گاما با پارامترهای shape = 1 و rate = 1 ایجاد کردم و آن را در بردار x ذخیره کردم. شما می‌توانید هر داده دیگری را به‌جای x بکار ببرید.

import numpy as np
#Create a sample data 
np.random.seed(123) 
x = np.random.gamma(shape = 1.0, scale = 1.0, size = 1000)

import numpy as np

#Create a sample data

np.random.seed(123)

x = np.random.gamma(shape = 1.0, scale = 1.0, size = 1000)

سپس از کتابخانه Scipy ماژول stats که عمدتاً برای محاسبات آماری در پایتون استفاده می‌شود، تابع boxcox را فراخوانی کردم. خروجی الگوریتم را در res ذخیره کردم و برآورد نقطه‌ای و بازه‌ای را به دست آوردم. همان‌طور که مشخص است لاندای بهینه برای این مثال حدود ۰٫۲۷ است.

#Box-Cox Transformation
from scipy.stats import boxcox
res = boxcox(x, alpha = 0.05)

#Point estimate of lambda
res[1]
0.26719468937166974

#Interval estimat of lambda
res[2]
(0.22604711942867162, 0.3094442740684491)

#Box-Cox transformation
trans_x = boxcox(x, lmbda = res[1])

#Box-Cox Transformation

from scipy.stats import boxcox

res = boxcox(x, alpha = 0.05)

#Point estimate of lambda

res[1]

0.26719468937166974

#Interval estimat of lambda

res[2]

(0.22604711942867162, 0.3094442740684491)

#Box-Cox transformation

trans_x = boxcox(x, lmbda = res[1])

درباره بررسی نرمال بودن داده‌ها در پایتون قبلاً همین مثال را حل کردم، بنابراین می‌توانید به آن مقاله مراجعه کنید.

منابع:

Daimon, T. (2011). “Box–Cox Transformation”, In: Lovric M. (eds), “International Encyclopedia of Statistical Science”, Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-04898-2_152

Sakia, R. M. (1992). “The Box–Cox Transformation Technique: A Review”, Statistician 41:169–۱۷۸

آنالیکا

مروری بر تبدیل Box-Cox و کاربردهای آن

تبدیل Box-Cox

پیاده‌سازی تبدیل Box-Cox در R

مثالی از کاربرد تبدیل Box-Cox در محاسبه ضریب همبستگی

تبدیل Box-Cox برای رگرسیون خطی

***ضمیمه: پیاده‌سازی تبدیل Box-Cox در پایتون

دیدگاهتان را بنویسید لغو پاسخ