در دنیای کسبوکار پیش میآید که تصمیمگیر به رابطه بین دو متغیر علاقهمند است. در آمار، از کوواریانس (Covariance) و همبستگی (Correlation) برای کمّی کردن رابطه بین متغیرها بهره میبرند. در این مقاله به تعاریف ریاضی این مفاهیم میپردازم. علاوه بر این با یک مثال در حوزه مدیریت کیفیت و اجرای آن در زبان R، کاربرد این مفهوم را در تصمیمگیری نشان خواهم داد.
کوواریانس نمونه آماری
کوواریانس یک شاخص توصیفی است که وجود رابطه خطی بین دو متغیر را سنجش میکند. اگر نمونهای آماری از متغیرهای و
دارای
مشاهده باشد، آنگاه کوواریانس بین این دو متغیر از رابطه زیر محاسبه میشود:

در فرمول بالا ابتدا فاصله هریک از مقادیر متغیرهای و
از میانگین آن محاسبه میشود. این انحرافها از میانگین برای مقادیر متناظر
و
در هم ضرب و مجموع آن محاسبه شده؛ سپس این مقدار بر
تقسیم میگردد.
همبستگی نمونه آماری
واحد کوواریانس تابع واحد متغیرهای و
است. به همین دلیل مقایسه این شاخص برای سنجیدن شدت رابطه بین متغیرها دشوار میشود. با تقسیم کوواریانس بر حاصلضرب انحراف معیار متغیرهای
و
ضریب همبستگی پیرسون (Pearson Correlation Coefficient) به دست میآید که تحت تأثیر واحد متغیرها نیست:
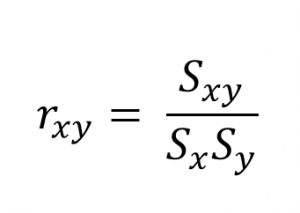
ضریب همبستگی همواره عددی بین ۱ و ۱- است. این ضریب دو بخش دارد: مقدار عددی و علامت. مقدار عددی نشان میدهد چقدر رابطه خطی بین دو متغیر قدرتمند است. علامت نشان میدهد جهت این رابطه مثبت است یا منفی.
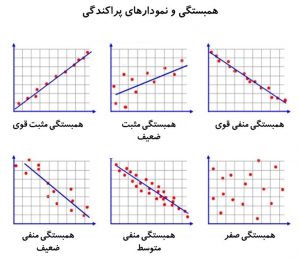
اگر ضریب همبستگی مثبت باشد، به این مفهوم است که افزایش در مقادیر یک متغیر با افزایش در مقادیر متغیر دیگر همراه است. همینطور کاهش در مقادیر یک متغیر با کاهش در مقادیر متغیر دیگر همراه است. در این حالت اگر نمودار پراکندگی دو متغیر رسم شود، میتوان خطی با شیب مثبت را از بین نقاط برازش داد (شکل-۱). به همین ترتیب اگر ضریب همبستگی منفی باشد، میتوان خطی با شیب منفی را از بین نقاط برازش داد (شکل-۱).
هرچه مقدار مطلق ضریب همبستگی (صرفنظر از علامت) به ۱ نزدیک باشد، نشان میدهد شدت رابطه خطی بین دو متغیر قویتر است. در مقابل ضریب همبستگی نزدیک صفر نشان میدهد که رابطه خطی بسیار ضعیفی بین متغیرهای و
برقرار است. در این حالت اگر نمودار پراکندگی دو متغیر رسم شود، اینطور به نظر میرسد نقاط به شکل تصادفی در صفحه رسم شدهاند (شکل-۱).
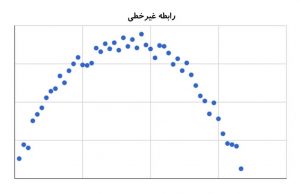
اگر بین دو متغیر رابطه غیرخطی برقرار باشد، همچنان این امکان وجود دارد ضریب همبستگی نزدیک صفر باشد که نشاندهنده نبود رابطه خطی بین دو آن است (شکل-۲). به همین دلیل در هنگام تحلیل بهتر است نمودار پراکندگی بین متغیرها رسم شود تا به وجود این روابط پی برد.
باید توجه کرد که اگر بین دو متغیر همبستگی دیده شود لزوماً به این معنی نیست که یکی دلیل وجود دیگری است. این امکان وجود دارد این همبستگی جعلی (Spurious Correlations) باشد به این معنی که متغیر پنهان سومی روی هر دو متغیر اثر میگذارد و یا اینکه همبستگی کاملاً تصادفی است.
برای توضیح بیشتر به مقاله ” چرا مدیران باید تفاوت بین همبستگی و رابطه علّی را بدانند؟” مراجعه کنید.
در نرمافزار اکسل (Excel) از تابع ()CORREL برای محاسبه ضریب همبستگی استفاده میشود. در شکل-۳ در خانه C12 از فرمول زیر برای محاسبه ضریب همبستگی بین متغیرهای X و Y استفاده شده است:
CORREL(B3:B10,C3:C10)=

یک مثال در حوزه مدیریت کیفیت
این مثال مربوط به خط تولید یک نوع ارهبرقی است که در آن از پرچ برای متصل کردن دو قطعه به یکدیگر استفاده میشود. یکی از شاخصهایی که جهت کنترل کیفیت در این خط تولید سنجیده میشود ارتفاع بیرونزدگی سر پرچ است. فرض کنید بهعنوان مدیر خط تولید، با بررسی روند موجود در نمودارهای کنترل کیفیت پی بردید که بهزودی ممکن است این ارتفاع از محدوده استاندارد خارج شود. در جلسهای که با تیم بهبود کیفیت خود دارید، یکی از اعضا پیشنهاد میدهد واریانس مشاهدهشده در فرآیند تولید، به علت ضخامت رنگی است که دور سوراخ پرچ مینشیند. رنگ زدن قطعات قبل از فرآیند پرچ اتفاق میافتد و بعد از آن ارتفاع پرچ سنجش میشود. با جمعآوری نمونه تصمیم میگیرید این فرضیه را بیازمایید که آیا بین ارتفاع پرچ (Rivet Height) و ضخامت رنگ (Paint Thickness) همبستگی وجود دارد یا خیر.
این مثال را در زبان R اجرا کردم. در ابتدا دادهها وارد و نمودار پراکندگی و خط رگرسیون رسم شده است (شکل-۴).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | #Input data Input = (" Paint_Thickness Rivet_Height 0.0008 0.0299 0.0010 0.0315 0.0009 0.0302 0.0008 0.0306 0.0011 0.0312 0.0016 0.0321 0.0011 0.0303 0.0013 0.0307 0.0009 0.0291 0.0010 0.0305 0.0010 0.0312 0.0007 0.0288 0.0009 0.0294 0.0016 0.0312 0.0012 0.0322 0.0011 0.0316 0.0012 0.0305 0.0008 0.0299 0.0011 0.0314 0.0010 0.0309 ") Data = read.table(textConnection(Input), header = TRUE) #Scatterplot plot(Rivet_Height ~ Paint_Thickness, data = Data, pch = 16) #Add regression line (y ~ x) abline(lm(Data$Rivet_Height ~ Data$Paint_Thickness), col = "red") |

برای محاسبه ضریب همبستگی پیرسون از کد زیر استفاده کردم:
1 2 3 | #Pearson Correlation cor(Data$Paint_Thickness, Data$Rivet_Height, method = "pearson") [1] 0.6684003 |
آزمون فرضیه برای ضریب همبستگی
ضریب همبستگی بالا نشان میدهد رابطه خطی نسبتاً قوی در نمونه آماری برقرار است. ولی آیا میتوان این رابطه مشاهدهشده در نمونه را به جامعه آماری گسترش داد و مدعی شد بین ارتفاع پرچ و ضخامت رنگ در فرآیند تولید همبستگی وجود دارد؟ برای پاسخ به این پرسش لازم است آزمون فرضیه را به ترتیب زیر انجام داد.
اول، باید فرض صفر (ضریب همبستگی در جامعه آماری () برابر صفر است) و فرض مقابل (ضریب همبستگی در جامعه آماری (
) مخالف صفر است) را تعیین کرد:
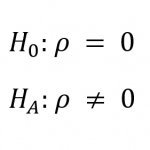
دوم، آماره آزمون را از رابطه زیر محاسبه کرد:
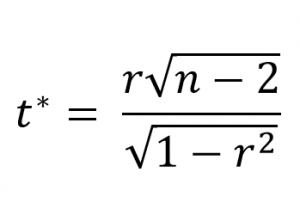
سوم، با محاسبه آماره آزمون، مقدار را محاسبه کرد. این مقدار از توزیع
با درجه آزادی
به دست میآید. این مقدار نشان میدهد اگر فرضیه صفر درست باشد با چه احتمالی آماره آزمون
به دست میآید.
چهارم، با مقایسه مقدار و سطح معنیداری
که معمولاً ۵ درصد در نظر گرفته میشود، تصمیم میگیریم آیا فرضیه صفر را میتوان رد کرد یا خیر. اگر مقدار
کوچکتر از ۵ درصد باشد، میتوان فرضیه صفر را رد کرد. بهاینترتیب میتوان گفت شواهد کافی وجود دارد که رابطه خطی بین متغیرها در جامعه آماری نیز برقرار و برآورد ما از ضریب همبستگی در جامعه (
) مقدار
است. اگر مقدار
بزرگتر از ۵ درصد باشد، به این معنی است که شواهد کافی برای رد کردن فرضیه صفر وجود ندارد و نمیتوانیم ادعا کنیم رابطه خطی بین دو متغیر در جامعه آماری برقرار است.
توجه شود که نتایج آزمون وقتی معتبر است که متغیرها بهصورت نرمال توزیع شده باشند.
در مثال بالا برای انجام آزمون فرضیه در R مراحل زیر را طی کردم.
ابتدا با آزمون Shapiro-Wilk فرض نرمال بودن دادهها را چک کردم. در این آزمون فرضیه صفر این است که دادهها به شکل نرمال توزیع شدند. فرضیه مقابل این است که دادهها به شکل نرمال توزیع نشدند.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | #Shapiro-Wilk normality test shapiro.test(Data$Paint_Thickness) Shapiro-Wilk normality test data: Data$Paint_Thickness W = 0.9077, p-value = 0.05763 shapiro.test(Data$Rivet_Height) Shapiro-Wilk normality test data: Data$Rivet_Height W = 0.97489, p-value = 0.8528 |
با مقایسه و سطح معنیداری ۵ درصد میتوان نتیجه گرفت متغیرهای حاضر در این مسئله از توزیع نرمال پیروی میکنند. پس میتوانیم از آزمون
استفاده کنیم. برای این منظور در R از کد زیر استفاده کردم:
1 2 3 4 5 6 7 8 9 10 11 12 13 | #Hypothesis test: Pearson Correlation cor.test(Data$Paint_Thickness, Data$Rivet_Height, method = "pearson") Pearson's product-moment correlation data: Data$Paint_Thickness and Data$Rivet_Height t = 3.8126, df = 18, p-value = 0.001275 alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval: 0.3207517 0.8573370 sample estimates: cor 0.6684003 |
از آنجا که مقدار از ۵ درصد کوچکتر است، میتوان نتیجه گرفت در جامعه آماری ارتفاع پرچ به شکل معنیداری باضخامت رنگ همبستگی دارد. برآورد ما از ضریب همبستگی مقدار ۰٫۶۶۸ است.
اگر با دادههای رتبهای (Ordinal) مواجه بودیم و یا دادهها بهصورت نرمال توزیع نشده بودند میتوان از ضریب همبستگی اسپیرمن (Spearman Correlation Coefficient) و یا ضریب همبستگی کندال (Kendall’s Tau Correlation Coefficient) استفاده کرد. هر دو ضریب همبستگی از رتبه مقادیر متغیرها برای محاسبه شدت رابطه بین دو متغیر استفاده میکنند. در مثال بالا میتوان با کدهای زیر آزمونهای همبستگی اسپیرمن و کندال را روی دادهها اجرا کرد. این آزمونها نیز نتایج مشابهی دارند و فرضیه صفر را رد میکنند.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | cor.test(Data$Paint_Thickness, Data$Rivet_Height, method = "spearman") Spearman's rank correlation rho data: Data$Paint_Thickness and Data$Rivet_Height S = 392.27, p-value = 0.0005169 alternative hypothesis: true rho is not equal to 0 sample estimates: rho 0.70506 > #Kendall rank correlation test cor.test(Data$Paint_Thickness, Data$Rivet_Height, method= "kendall") Kendall's rank correlation tau data: Data$Paint_Thickness and Data$Rivet_Height z = 3.2341, p-value = 0.00122 alternative hypothesis: true tau is not equal to 0 sample estimates: tau 0.5526062 |
منابع:
Sheskin, D. J. (2000). “Parametric and Nonparametric Statistical Procedures”, Chapman & Hall/CRC: Boca Raton, FL
Wilcox, R. R. (2016). “Understanding and Applying Basic Statistical Methods Using R”, John Wiley & Sons

سلام.احسنت
بسیار عالی و روان و ساده توضیحات داده شده و یک سایت کم نظیر دارید و تبریک میگویم.
حسین زینل
مشاور سیستمهای کیفیت آزمایشگاهی
سلام بسیار عالی و ساده و روان بود احسنت
سلام ببخشید میخواستم بدونم از سیستم rho برای تسویه آب صنعتی میشود استفاده کرد
سلام توضیحات برای ضریب همبستگی خیلی ساده و عالی بود