رمزنگاری کلید عمومی و امضاء دیجیتال

در مقاله “مقدمه‌ای بر مفاهیم رمزنگاری” بحث کردم که تا مدت‌ها، انسان از روش رمزنگاری متقارن (Symmetric Cryptography) برای پنهان کردن پیام استفاده می‌کرد. در این روش گیرنده با همان کلیدی که فرستنده، پیام را رمزنگاری کرده، آن را رمزگشایی می‌کند. برای این منظور باید هردو طرف از قبل این کلید را از طریق یک کانال ایمن باهم مبادله کنند؛ اما اگر دو طرف از قبل یکدیگر را نشناسند و هیچ ارتباطی پیش از مبادله پیام باهم نداشته باشند چه باید کرد؟

در آن مقاله اشاره کردم یک راهکار استفاده از الگوریتم مبادله کلید دیفی-هلمن (Diffie-Hellman Key Exchange) است. این الگوریتم به طرفین اجازه می‌دهد که یک کلید عمومی (Public Key) را با یکدیگر به اشتراک بگذارند تا پیام تنها توسط کسی که کلید خصوصی (Private Key) معادل آن کلید عمومی را دارد، رمزگشایی شود. این الگوریتم دو طرف را به یک کلید رمز مشترک می‌رساند بدون آنکه شنودکننده بتواند به آن پی ببرد.

در این روش اگر فرستنده بخواهد با تعداد زیادی از افراد پیام مبادله کند باید برای هر مبادله یک کلید عمومی متمایز داشته باشد. برای مثال درگاه پرداخت بانکی که افراد مختلف در روز به آن سر می‌زنند و اطلاعات باید به‌صورت رمزنگاری‌شده بین سرور درگاه پرداخت و کامپیوتر کاربران مبادله شود. آیا می‌توان روش ساده‌تری را تصور کرد که در آن بانک تنها نیاز به یک کلید عمومی برای مبادله پیام با همه کاربرانش داشته باشد؟ الگوریتم رمزنگاری RSA راهکاری برای مواجهه با این مشکل است.

نکته مهم دیگر این‌که در الگوریتم مبادله کلید دیفی-هلمن، پیام در داخل الگوریتم وارد نمی‌شود و تنها از آن می‌توان برای دست یافتن به کلید رمز مشترک استفاده کرد. درحالی‌که در الگوریتم RSA خود پیام نیز رمزگذاری و مبادله می‌شود.

رمزنگاری RSA

ایده پشت رمزنگاری RSA ساده درعین‌حال هوشمندانه است. من در اینجا مشابه مقاله قبل از استعاره رنگ‌ها بهره می‌برم. با استفاده از استعاره رنگ‌ها مسئله به‌این‌ترتیب درمی‌آید که چگونه فرد ب در حضور شنودکننده یک رنگ (مثلاً رنگ زرد) را برای فرد الف بفرستد بدون آنکه شنودکننده متوجه آن رنگ شود. در اینجا رنگ زرد پیامی است که قرار است فرد ب به فرد الف بفرستد.

قبل از آنکه وارد توضیح الگوریتم شوم باید به یک تعریف بپردازم. مکمل یک رنگ به رنگی گفته می‌شود که اگر با رنگ اصلی ترکیب شود، حاصل آن رنگ سفید است. به عبارتی اثر رنگ اصلی را خنثی می‌کند. مشابه الگوریتم مبادله کلید دیفی-هلمن در اینجا هم فرض می‌شود که ترکیب رنگ‌ها فرآیندی آسان است. در مقابل فرآیند معکوس، یعنی رسیدن از رنگ ترکیبی به رنگ‌های تشکیل‌دهنده، کار دشوار و زمان بری است.

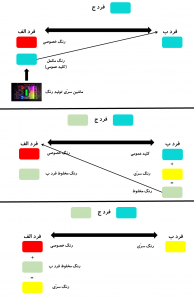
شکل-۱ مراحل رمزنگاری RSA را با استفاده از استعاره رنگ‌ها نشان می‌دهد. فرض کنید فرد ب می‌خواهد یک رنگ سرّی، در اینجا رنگ زرد را به فرد الف بفرستد. در گام اول فرد الف با انتخاب یک رنگ به شکل تصادفی یک کلید خصوصی (رنگ قرمز) تولید می‌کند و آن را نزد خود نگه می‌دارد. فرد الف یک ماشین تولید رنگ مخفی دارد که رنگ مکمل هر رنگی را تولید می‌کند. فرد الف رنگ مکمل رنگ خصوصی خود را به دست می‌آورد و آن را برای فرد ب می‌فرستد. این رنگ همان کلید عمومی فرد الف است. با ارسال این رنگ به فرد ب، شنودکننده (فرد ج) هم به این کلید عمومی دست پیدا می‌کند. حال فرد ب این رنگ عمومی را با رنگ سرّی که می‌خواهد برای فرد الف بفرستد ترکیب می‌کند. سپس این رنگ مخلوط را برای فرد الف می‌فرستد. شنودکننده به این رنگ نیز دسترسی دارد. در گام آخر فرد الف رنگ خصوصی خود را با رنگ مخلوط فرد ب ترکیب می‌کند. این باعث می‌شود اثر رنگ عمومی خودش از رنگ مخلوط فرد ب خنثی شود و به رنگ سرّی که همان زرد است برسد.

شنودکننده با داشتن رنگ عمومی و رنگ مخلوط فرد ب نمی‌تواند به رنگ سرّی دست پیدا کند چراکه رنگ خصوصی فرد الف (رنگ قرمز) را در دست ندارد. این استدلال با این فرض درست است که پیدا کردن اجزاء تشکیل‌دهنده رنگ‌های ترکیب‌شده دشوار است.

این الگوریتم برای اولین بار توسط سه محقق به نام‌های ران ریوست (Ron Rivest)، آدی شامیر (Adi Shamir) و لئونارد ادلمن (Leonard Adleman) ارائه شد. نام این الگوریتم برگرفته از حروف ابتدای نام خانوادگی این افراد است. خوانندگان علاقه‌مند می‌توانند بخش ضمیمه مقاله را برای آشنایی با روش ریاضی این الگوریتم مطالعه کنند.

توابع درهم‌سازی

امروزه توابع درهم‌سازی (Hash Functions) نقش مهمی در رمزنگاری دارند. یک تابع درهم‌سازی زنجیره‌ای از اعداد و حروف را می‌گیرد و یک خروجی یکتا با طول ثابت می‌دهد. این خروجی عددی با طول ثابت، می‌تواند در داخل سایر الگوریتم‌های رمزنگاری استفاده شود.

یکی از توابع پرکاربرد درهم‌سازی، الگوریتم SHA-256 نام دارد که در رمزگذاری پیام‌ها در بیت‌کوین (Bitcoin) نیز استفاده می‌شود. برای مثال پیام “سلام خوبی؟” با استفاده از الگوریتم SHA-256 خروجی زیر را می‌دهد:

$2d8771124f9f6b96dec0a69a1751edd247cae5fa71203ca8c4d9c70573320909$

به خروجی این توابع، هَش (Hash) گفته می‌شود. می‌توانید به آدرس زیر مراجعه کنید و پیام دلخواه خود را بنویسید و خروجی آن را با استفاده از این الگوریتم مشاهده کنید:

https://tools.superdatascience.com/blockchain/hash/

توابع درهم‌سازی دارای چند ویژگی مهم هستند:

اول، خروجی آن برای یک زنجیره ورودی مشخص هیچ‌گاه تغییر نمی‌کند. اگر یک پیام را بارها و بارها به تابع درهم‌سازی بدهید، همواره خروجی یکسانی دریافت می‌کنید.

دوم، محاسبه مسیر معکوس بسیار دشوار است. اگر خروجی یک تابع درهم‌سازی را داشته باشید، تقریباً ناممکن است تا ورودی متناظر را پیدا کنید.

سوم، کوچک‌ترین تغییری در زنجیره ورودی، خروجی را به‌طور کل تغییر می‌دهد. برای مثال اگر پیام من به شکل “سلم خوبی؟” درآید، خروجی تابع SHA-256 آن به شکل زیر است:

$2dd017e2c430dc48d30dde77b4589cb3b49868f860cb5b32189e2ef87ed8bb2b$

همان‌طور که می‌بینید این خروجی کاملاً متفاوت از قبلی است. این ویژگی موجب می‌شود حدس زدن خروجی یک زنجیره ورودی از روی زنجیره ورودی مشابه امکان‌پذیر نباشد.

نام SHA از سرواژه عبارت Secure Hash Algorithm گرفته شده است. عدد ۲۵۶ بیانگر این است که خروجی این تابع همواره ۲۵۶ بیت از حافظه اشغال می‌کند. علت این است که خروجی تابع SHA-256 عددی ۶۴ رقمی در مبنای شانزده (Hexadecimal) است. می‌دانیم هر نماد ۴ بیت از حافظه کامپیوتر را اشغال می‌کند پس درمجموع یک خروجی ۶۴ رقمی ۲۵۶ بیت از حافظه را به خود اختصاص می‌دهد.

لازم به ذکر است که در مبنای ۱۶، از شانزده نماد برای نشان دادن اعداد استفاده می‌شود. چنانکه در مبنای ۱۰ با استفاده از اعداد ۰ تا ۹ می‌توان همه اعداد را نشان داد. در مبنای ۱۶، نمادهای ۰ تا ۹ نشان‌دهنده مقادیر ۰ تا ۹ هستند و نمادهای A تا F نشان‌دهنده مقادیر ۱۰ تا ۱۵ هستند. برای نمونه عدد ۱۳۸۱۹۷ در سیستم ده‌دهی معادل $21bd5$ در مبنای شانزده است.

هر سند دیجیتال (متن، صوت، ویدئو و غیره) را که وارد الگوریتم SHA-256 کنید یک عدد ۶۴ رقمی در مبنای شانزده دریافت می‌کنید. برای هر میزان از ورودی، طول خروجی تابع ثابت است.

چقدر الگوریتم SHA-256 قابل‌اطمینان است؟ اگر یک فرد و گروهی بخواهند تمام حالت‌های ممکن برای خروجی‌های این تابع را به دست آورند چقدر طول می‌کشد؟ پاسخ این سؤال بستگی به قدرت محاسباتی ماشین‌های هر زمان دارد؛ اما برای این‌که خواننده بتواند مقیاسی از احتمال وقوع آن به دست آورد من محاسباتی را انجام دادم.

ازآنجاکه خروجی تابع SHA-256 یک عدد ۶۴ رقمی است و هر رقم ۱۶ حالت مختلف می‌تواند به خود بگیرد، درمجموع ۱۶ به توان ۶۴ یا ۲ به توان ۲۵۶ حالت مختلف برای خروجی وجود دارد. درزمانی که این مقاله را می‌نویسم (خردادماه ۱۳۹۷) در شبکه بیت‌کوین ۴۰ میلیون تریلیون ( $40\times10 ^{18}$ ) هَش در هر ثانیه تولید می‌شود (شکل-۲). برای آگاهی از نرخ تولید هَش در هرلحظه می‌توانید به آدرس زیر مراجعه کنید:

https://blockchain.info/charts/hash-rate

اگر فرض کنیم تولید هَش با همین سرعت در شبکه بیت‌کوین ادامه پیدا کند، پس از چند سال همه حالت‌های ممکن به پایان می‌رسد؟ محاسبات زیر نتیجه را به دست می‌دهد:

$2 ^{256}/(40\times10 ^{18}\times86400\times365.25)=9.173\times10 ^{49}$

برای آنکه بزرگی این عدد را درک کنید، یادآوری می‌کنم برآورد از عمر کل جهان هستی ۱۳٫۷۷۲ میلیارد ( $13.772\times10 ^{9}$ ) سال است.

بنابراین قابل‌تصور است با روش جستجو نمی‌توان به‌راحتی SHA-256 را شکست. گرچه نسل‌های قدیمی‌تر توابع درهم‌سازی شکسته شده‌اند تا امروز گزارشی از شکسته شدن SHA-256 منتشر نشده است. ضمن اینکه نسل‌های جدید توابع درهم‌سازی نیز درحال ‌توسعه یا به‌کارگیری هستند.

امضاء دیجیتال

فرض کنید الف کلید عمومی ب را دارد و می‌خواهد برای او پیامی بفرستد. در عصر شبکه‌های کامپیوتری معمولاً الف و ب از قبل هیچ ارتباطی با یکدیگر نداشتند و همدیگر را نمی‌شناسند. پس ج (شنودکننده) هم که کلید عمومی ب را دارد، می‌تواند وانمود کند که الف است و برایش پیام رمزگذاری شده بفرستد. بنابراین نیاز است تا هویت ارسال‌کننده تائید شود؛ مشابه حالت کاغذی که شما هویت نویسنده یک نوشته را از روی امضاء یا مهر زیر آن تشخیص می‌دهید. به همین دلیل این مفهوم امضاء دیجیتال (Digital Signature) نام گرفته است.

در حالت کاغذی، رسم‌الخط خاص امضاء شما به‌نوعی بازتاب‌دهنده هویت‌تان است. وقتی متنی را امضاء می‌کنید این هویت را به نوشته پیوند می‌زنید. هرچه امضاء شما خاص‌تر و دشوارتر باشد، امکان این‌که شخص دیگری بتواند آن را جعل کند و هویت‌تان را برباید، سخت‌تر می‌شود.

در امضاء دیجیتال فرآیند مشابهی بر اساس الگوریتم‌های ریاضی صورت می‌گیرد. یکی از این‌ها، الگوریتم RSA است که در امضاء دیجیتال هم بکار می‌رود. فرض کنید الف می‌خواهد به ب یک پیام رمزگذاری شده با امضاء دیجیتال بفرستد. الف می‌تواند از کلید خصوصی خودش بهره گیرد تا پیام خود را امضاء دیجیتالی کند. او ابتدا پیام را وارد تابع درهم‌سازی و مقدار هَش آن را دریافت می‌کند. سپس مقدار هَش را به همراه کلید خصوصی خودش وارد یک تابع ریاضی می‌کند. خروجی یک امضاء دیجیتال است. به شکل ساده‌شده امضاء دیجیتال از یک تابع ریاضی به شکل زیر به دست می‌آید:

می‌توانید به آدرس زیر بروید و با شبیه‌ساز امضاء دیجیتال کار کنید:

https://tools.superdatascience.com/blockchain/public-private-keys/signatures

در شبیه‌ساز بالا، به بخش Sign رفته و یک پیام دلخواه بنویسید و با استفاده از کلید خصوصی تولیدشده آن را امضاء دیجیتالی کنید (شکل-۳). توجه کنید شبیه‌ساز معرفی‌شده تنها برای نشان دادن کارکرد امضاء دیجیتال است و خود پیام رمزگذاری نمی‌شود.

ب پیام امضاءشده را دریافت کرده، آن را به همراه کلید عمومی الف و امضاء دیجیتال وارد یک تابع ریاضی دیگر می‌کند تا هویت ارسال‌کننده را مشخص کند. به شکل ساده‌شده تائید هویت از یک تابع ریاضی به شکل زیر به دست می‌آید که خروجی آن صفر (عدم تائید) یا یک (تائید) است:

در اینجا ج (شنودکننده) چون به کلید خصوصی متناظر با کلید عمومی الف دسترسی ندارد، نمی‌تواند پیامی با امضاء دیجیتال بفرستد و خود را الف جا بزند. همین‌طور توجه کنید که امضاء دیجیتال تابع پیام نیز هست. به‌این‌ترتیب کوچک‌ترین دست‌کاری در پیام اصلی توسط شنودکننده، آن را از اعتبار می‌اندازد.

در شبیه‌ساز معرفی‌شده، به بخش Verify رفته و پیام را تائید کنید؛ صفحه به رنگ سبز درمی‌آید. برای امتحان تغییری کوچکی در پیام اصلی ایجاد کنید. مشاهده می‌کنید که پیام تائید نمی‌شود. تغییری کوچکی در کلید عمومی فرد الف ایجاد کنید، بازهم پیام تائید نمی‌شود. اگر به صفحه Sign برگردید و تغییری در کلید خصوصی فرد الف ایجاد کنید و دوباره به صفحه Verify برگردید، بازهم پیام تائید نمی‌شود چراکه کلید عمومی دیگر متناظر با آن کلید خصوصی نیست. تمامی این حالت‌ها در شکل-۴ نشان داده شده‌اند.

امروزه امضاء دیجیتال بر روی بسترهای الکترونیکی تبادل اطلاعات در حوزه‌های مختلف بخصوص تبادلات مالی استفاده می‌شود. با فراگیر شدن اسناد دیجیتال، امضاء دیجیتال را می‌توان برای اطمینان از احراز هویت، بیان تائید و ابراز رضایت از یک سند بکار برد. برای این منظور باید زیرساخت‌های فنی و حقوقی فراهم باشد تا آن را ممکن کند. خوشبختانه در ایران در قانون تجارت الکترونیک مصوب ۱۳۸۲، امضاء دیجیتال به رسمیت شناخته شده است و شما می‌توانید با مراجعه به دفتر اسناد رسمی آن را دریافت کنید. باوجود فراهم بودن زیرساخت‌های قانونی و فنی، به نظر می‌رسد همچنان در ایران فضا برای به‌کارگیری گسترده‌تر امضاء دیجیتال وجود دارد.

***ضمیمه: الگوریتم RSA

مشابه الگوریتم مبادله کلید دیفی-هلمن، این الگوریتم نیز به دنبال راه‌حلی است که محاسبه در مسیر رفت ساده ولی در مسیر معکوس دشوار باشد. الگوریتم RSA نیز بر پایه ریاضیات همنهشتی (Modular Arithmetic) بنا نهاده شده است. فرض کنید فرد ب می‌خواهد پیام $m$ را در حضور شنودکننده به فرد الف برساند. او پیام را به توان کلید عمومی فرد الف ( $e$ ) می‌رساند و حاصل را در پیمانه $n$ محاسبه می‌کند تا $c$ به دست آید. سپس او مقدار $c$ را برای الف می‌فرستد.

$m ^{e}\equiv c (mod_{n})$

فرد الف $c$ را گرفته به توان کلید خصوصی خود ( $d$ ) می‌رساند و پیام ظاهر می‌شود. در اینجا فرآیند ریاضی باید به‌گونه‌ای باشد که تنها کسی که کلید خصوصی متناظر کلید عمومی را دارد بتواند پیام را رمزگشایی کند.

$c^{d}\equiv (m^{e}) ^{d}\equiv m ^{e\times d}\equiv m (mod_{n})$

پرسش این است که $e$ و $d$ چگونه انتخاب شوند تا رابطه بالا برقرار شود، با در نظر گرفتن این‌که شنودکننده به $n$ ، $e$ و $c$ دسترسی دارد و نباید بتواند در یک‌زمان معقول فرآیند معکوس را طی کند. یعنی باید شرایط زیر برقرار باشد:

ساده:

$m ^{e}\equiv \Rightarrow?(mod_{n})$

دشوار:

$? ^{e}\equiv \Leftarrow c(mod_{n})$

به تابعی که در یک‌سو به‌آسانی محاسبه شده و در سوی مخالف محاسبهٔ آن برای پردازنده‌ها بسیار دشوار است، تابع دریچه (Trapdoor Function) گفته می‌شود. در استعاره رنگ‌ها که در ابتدای مقاله استفاده کردم، ماشین مخفی تولید رنگ نقش تابع دریچه را دارد.

الگوریتم RSA از ویژگی‌های اعداد اول برای ساختن تابع دریچه استفاده می‌کند. برای این منظور لازم است با تابع فی اویلر (Euler’s Phi Function) و ویژگی‌های آن آشنا بود.

در نظریه اعداد، تابع فی اویلر، $\varphi(n)$ ، تابعی است که تعداد اعداد طبیعی کوچک‌تر از $n$ را که نسبت به $n$ اول‌ هستند، می‌شمارد. برای مثال داریم:

$\phi(8)=4$

چراکه چهار عدد ۱، ۳، ۵ و ۷ هستند که با عدد ۸ هیچ عامل مشترکی ندارند. شکل-۵ نمودار تابع فی را برای اعداد کوچک‌تر از ۱۰۰۰ نشان می‌دهد. همان‌طور که مشخص است این تابع از هیچ الگوی خاصی پیروی نمی‌کند. تنها به نظر می‌رسد حد بالایی آن یک خط مستقیم را نشان می‌دهد. این‌ها اعداد اول (Prime Numbers) هستند. یک عدد اول تنها بر خودش و ۱ بخش‌پذیر است؛ بنابراین نسبت به ‌تمامی اعداد قبل از خودش اول است. پس به ازای هر عدد اول $p$ رابطه زیر برقرار است:

$\phi(p)=p-1$

همچنین تابع فی اویلر یک تابع ضربی است، بدین معنی که اگر دو عدد $m$ و $n$ نسبت به هم اول باشند آنگاه:

$\phi(m\times n)=\phi(m)\times\phi(n)$

به‌این‌ترتیب تابع فی برای ضرب دو عدد اول $p_{{1}}$ و $p_{{2}}$ به شکل زیر محاسبه می‌شود:

$\phi(p_{1}\times p_{2})=(p_{1}-1)\times(p_{2}-1)$

تابع فی یک ویژگی مهم دیگر نیز دارد که در قضیه اویلر (Euler’s Theorem) بکار می‌رود. اگر $n$ و $a$ نسبت به هم اول باشند آنگاه داریم:

$a^{\phi(n)}\equiv 1(mod_{n})$

چگونه از این ویژگی‌ها برای ساختن تابع دریچه استفاده کنیم؟ اول، اگر دو عدد اول تصادفی ( $p_{{1}}$ و $p_{{2}}$ ) بسیار بزرگ داشته باشیم به‌راحتی می‌توان آن‌ها را در هم ضرب کرد ( $n=p_{{1}}\times p_{{2}}$ ). ولی با داشتن حاصل‌ضرب ( $n$ ) صدها هزار سال طول می‌کشد تا بتوان آن دو عدد را پیدا کرد. دوم، قضیه اویلر کمک می‌کند تا اعداد اول را به ریاضیات همنهشتی که در ابتدای بحث اشاره کردم، ارتباط داد. اگر $m$ پیام باشد (توجه کنید پیام به شکل عددی در آمده است) و $m$ و $n$ نسبت به هم اول باشند، طبق قضیه اویلر داریم:

$m^{\phi(n)}\equiv 1(mod_{n})$

حال اگر طرفین را به توان عدد طبیعی $k$ برسانیم و در $m$ ضرب کنیم، رابطه به شکل زیر در می‌آید:

$m^{k\times\phi(n)+1}\equiv m(mod_{n})$

پس کافی است داشته باشیم:

$e\times d=k\times\phi(n)+1$

به‌این‌ترتیب رابطه کلید خصوصی ( $e$ ) و کلید عمومی متناظر ( $d$ ) مشخص می‌شود.

مراحل کار الگوریتم RSA به شرح زیر است:

دو عدد اول بزرگ و متمایز $p_{{1}}$ و $p_{{2}}$ را به‌صورت تصادفی بیابید.

عدد n را محاسبه کنید به‌طوری‌که

$n=p_{{1}}\times p_{{2}}$

تابع فی را برای مقدار $n$ محاسبه کنید:

$\phi(n)=(p_{1}-1)\times(p_{2}-1)$

عدد طبیعی $e$ را انتخاب کنید به‌طوری‌که:

$1<e<\phi(n)$

و همچنین $e$ و $\phi(n)$ نسبت به هم اول باشند.

بر اساس رابطه بیان‌شده، مقدار متناظر کلید خصوصی را پیدا کنید:

$d=(k\times\phi(n)+1)/e$

مقادیر $e$ و $n$ به‌عنوان کلید عمومی فرد الف اعلام ‌شود.

فرد ب پیام خود ( $m$ ) را به توان $e$ می‌رساند و حاصل را در پیمانه $n$ محاسبه می‌کند تا $c$ به دست آید. سپس او مقدار $c$ را برای الف می‌فرستد.

$m ^{e}\equiv c (mod_{n})$

حال الف از کلید خصوصی خود ( $d$ ) استفاده می‌کند و $c$ را به توان $d$ می‌رساند و حاصل را در پیمانه $n$ محاسبه می‌کند تا پیام را باز یابد.

$c^{d}\equiv (m^{e}) ^{d}\equiv m ^{e\times d}\equiv m ^{k\times\phi(n)+1}\equiv m (mod_{n})$

شنودکننده گرچه به $n$ ، $e$ و $c$ دسترسی دارد، ولی نمی‌تواند $d$ را پیدا کند. برای پیدا کردن $d$ او باید دو عدد اول تشکیل‌دهنده $n$ را بیابد که همان‌طور که گفتم کار بسیار دشواری است.

منابع:

Callas, J. (2008). “An Introduction to Cryptography”, PGP Corporation

Ferguson, N., Schneier, B., & Kohno, T. (2011). “Cryptography Engineering: Design Principles and Practical Applications”, John Wiley & Sons

SURF (2010). “Applications of Modern Cryptography: Technologies, Applications and Choices”, https://www.surf.nl/binaries/content/assets/surf/en/knowledgebase/2010/rapport_201009_SNcryptoWEB.pdf

آنالیکا

رمزنگاری کلید عمومی و امضاء دیجیتال

رمزنگاری RSA

توابع درهم‌سازی

امضاء دیجیتال

***ضمیمه: الگوریتم RSA

دیدگاهتان را بنویسید لغو پاسخ