الگوریتم گرادیان کاهشی چیست؟

در بسیاری از الگوریتم‌های یادگیری ماشین (Machine Learning) عملاً یک مسئله بهینه‌سازی حل می‌شود. برای مثال در مسائل رگرسیون (Regression) هدف آن است که فاصله مقدار پیش‌بینی‌شده توسط الگوریتم یادگیری ماشین از مقدار واقعی آن کمینه شود. ازآنجاکه بسیاری از الگوریتم‌های یادگیری ماشین در کامپیوتر با روش‌های عددی پیاده‌سازی می‌شوند، الگوریتم گرادیان کاهشی (Gradient Descent) که با یک روش تکرارشونده خود را به مقدار بهینه نزدیک می‌کند، بسیار کاربردی است. در این مقاله به زبان ساده الگوریتم گرادیان کاهشی را توضیح خواهم داد.

رویکردهای محاسبات عددی در حل مسائل بهینه‌سازی، به دو دسته عمده تقسیم می‌شوند: رویکردهای بدون استفاده از مشتق (Derivative-free Methods) و رویکردهای مبتنی بر مشتق‌گیری (Derivative Methods).

در رویکرد اول مشتق‌گیری از تابع کاربرد ندارد، الگوریتم‌هایی مانند Golden Section Search و Successive Parabola Interpolation در این دسته جای می‌گیرند. در رویکرد دوم، مشتق تابع به‌نوعی استفاده می‌گردد. الگوریتم گرادیان کاهشی در این دسته جای دارد. بنابراین در این رویکرد فرض مشتق‌پذیری تابع نیاز است.

تابع زیر را در بازه ۶- تا ۲+ در نظر بگیرید (شکل-۱):

$f(x) = x ^ 4 + 7 x ^ 3 + 5 x ^ 2 - 17 x + 3$

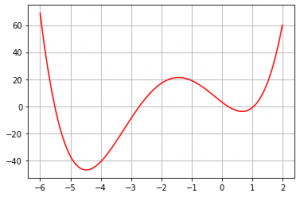
هدف آن است تا کمینه این تابع را در بازه مذکور به دست آوریم. در حل مسائل بهینه‌سازی معمولاً فرض می‌شود که هدف پیدا کردن کمینه تابع است. واضح است که برای پیدا کردن بیشینه تابع $f(x)$ کافی است الگوریتم را برای پیدا کردن کمینه تابع $-f(x)$ بکار ببریم.

درک شهودی از الگوریتم گرادیان کاهشی

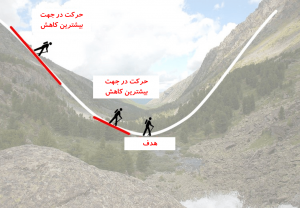
رویکردی که الگوریتم گرادیان کاهشی برای حل مسئله به کار می‌برد بسیار ساده و قابل‌فهم است. برای درک شهودی از این الگوریتم فرض کنید در یک کوهستان جنگلی مه‌آلود مانند شکل-۲ گیر افتادید و می‌خواهید راه خود را به سمت خط‌ القعر کوهستان پیدا کنید. چراکه با احتمال زیاد در خط القعر کوهستان رودخانه‌ای جریان دارد و با دنبال کردن رودخانه به یک آبادی می‌رسید.

الگوریتم گرادیان کاهشی در چنین شرایطی توصیه می‌کند که در آن نقطه‌ای که هستید به‌صورت ۳۶۰ درجه به اطراف خودتان نگاه کنید. طبیعتاً چون نمی‌توانید تا دوردست‌ها را ببینید فقط محدوده چندمتری اطراف شما مشخص است. سپس بررسی کنید اگر در کدام جهت حرکت کنید بیشترین کاهش ارتفاع را تجربه خواهید کرد. چند گام در آن جهت حرکت کنید.

به‌این‌ترتیب شما در یک نقطه جدید قرار می‌گیرید. دوباره در نقطه جدید ۳۶۰ درجه به اطرافتان نگاه و در جهتی حرکت کنید که بیشترین کاهش ارتفاع ایجاد می‌شود. چند گام در آن جهت حرکت کنید و دوباره در نقطه جدید اطرافتان را بررسی و جهت حداکثر کاهش ارتفاع را شناسایی کنید. با ادامه این روند شما به‌تدریج به خط القعر کوهستان می‌رسید (شکل-۳).

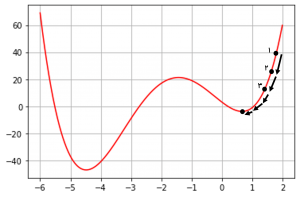
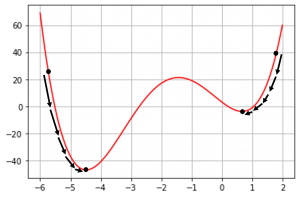
همین رویکرد را می‌توان برای پیدا کردن نقطه کمینه تابع $f(x)$ استفاده کرد. فرض کنید در نقطه ۱ ایستادیم (شکل-۴). در این مثال دو گزینه داریم. از نقطه ۱ به سمت چپ یا به سمت راست برویم. از روی تصویر مشخص است که حرکت به سمت چپ باعث کاهش $f(x)$ می‌شود، پس یک گام به سمت چپ حرکت می‌کنیم.

از منظر ریاضی اگر بخواهیم متوجه شویم باید به سمت راست یا چپ حرکت کنیم، نیاز است به مشتق تابع در آن نقطه نگاه کنیم. به زبان ساده، مشتق تابع در هر نقطه نشان می‌دهد اگر به‌اندازه $\Delta x$ به $x$ اضافه شود، $f(x)$ زیاد خواهد شد یا کم. اگر دقت کنید شیب‌خط مماس در نقطه ۱ مثبت است؛ یعنی کاهش $x$ در نقطه ۱ (حرکت به سمت چپ) موجب کاهش $f(x)$ می‌شود.

به‌این‌ترتیب با حرکت به سمت چپ از نقطه ۱ به نقطه ۲ می‌رسیم. بطور مشابه در نقطه ۲ حرکت به سمت چپ، موجب کاهش $f(x)$ می‌شود. پس به سمت چپ حرکت کرده و به نقطه ۳ می‌رسیم. این کار را ادامه می‌دهیم تا به نقطه کمینه نسبی تابع $f(x)$ می‌رسیم. در آن نقطه حرکت به سمت چپ و یا راست هیچ‌کدام باعث کاهش $f(x)$ نمی‌شود و الگوریتم در نقطه کمینه نسبی متوقف می‌گردد.

نکته قابل‌توجه این است که بسته به اینکه الگوریتم از چه نقطه اولیه‌ای شروع می‌شود، ممکن است به کمینه‌های نسبی متفاوتی همگرا شود (شکل-۵). دراین‌باره بیشتر صحبت خواهم کرد.

الگوریتم گرادیان کاهشی برای توابع چندمتغیره

مثال بالا برای یک تابع یک متغیره بود. این رویکرد را می‌توان برای توابع چندمتغیره بکار برد. تنها نکته آن است که از بردار گرادیان (Gradient Vector) باید استفاده کرد. بردار گرادیان مشتقات پاره‌ای تابع $f$ را نسبت به متغیرهایش در هر نقطه محاسبه می‌کند:

$\bigtriangledown f(x_{1}, x_{2}, ..., x_{n}) = (\frac{\partial f}{\partial x_{1}}, \frac{\partial f}{\partial x_{2}}, ..., \frac{\partial f}{\partial x_{n}})$

اگر از ریاضیات پایه یادتان باشد، جهت بردار گرادیان در هر نقطه جهت حداکثر افزایش تابع $f$ را نشان می‌دهد. برای مثال اگر تابع $f$ یک تابع دومتغیره به شکل زیر باشد:

$f(x, y) = x ^ 2 + y ^2$

بردار گرادیان آن در هر نقطه به شکل زیر خواهد بود:

$\bigtriangledown f(x,y) = (\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}) = (2x, 2y)$

برای نقطه $(1.1, -0.3)$ بردار گرادیان به‌صورت زیر خواهد بود:

$\bigtriangledown f(x,y) = (2.2, -0.6)$

اگر در نقطه $(1.1, -0.3)$ در جهت این بردار حرکت کنیم، بیشترین افزایش را در $f$ تجربه خواهیم کرد و اگر در خلاف جهت این بردار حرکت کنیم، بیشترین کاهش را در $f$ خواهیم دید (شکل-۶).

بنابراین در الگوریتم گرادیان کاهشی برای پیدا کردن جهت حداکثر کاهش در $f$ در هر نقطه، کافی است خلاف جهت گرادیان حرکت کنیم. فرمول‌بندی ریاضی الگوریتم گرادیان کاهشی به‌صورت زیر است:

$x_{i + 1} = x_{i} - \gamma \bigtriangledown f(x_{i})$

رابطه بالا به این معنی است در هر تکرار الگوریتم، از نقطه‌ای که ایستادیم ( $x_{i}$ ) به‌اندازه یک گام مشخص ( $\gamma$ ) در خلاف جهت گرادیان در آن نقطه ( $\bigtriangledown f(x_{i})$ ) حرکت می‌کنیم و به نقطه جدید ( $x_{i + 1}$ ) می‌رسیم.

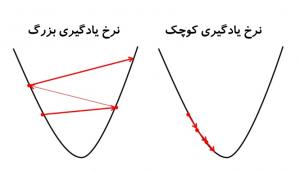
به $\gamma$ نرخ یادگیری می‌گویند. نرخ یادگیری تعیین می‌کند در هر تکرار چقدر در جهت کاهش گرادیان حرکت شود. اگر نرخ یادگیری خیلی کوچک باشد، منجر به این می‌شود که الگوریتم خیلی کند به نقطه کمینه نسبی همگرا شود و اگر خیلی بزرگ باشد ممکن است الگوریتم واگرا شود (شکل-۷). معمولاً نرخ یادگیری بین ۰٫۰۰۱ تا ۰٫۳ تعیین می‌شود.

پیاده‌سازی الگوریتم گرادیان کاهشی در پایتون

در این بخش من می‌خواهم به مسئله اولیه‌ای که مطرح کردم برگردم و کمینه مطلق تابع $f(x)$ را با الگوریتم گرادیان کاهشی پیدا کنم.

در ابتدا من تابع $f(x)$ و مشتق آن $g(x)$ را تعریف کردم:

def f(x):
    return(x ** 4 + 7 * x ** 3 + 5 * x ** 2 - 17 * x + 3)

#Gradient of f
def g(x):
    return(4 * x ** 3 + 21 * x ** 2 + 10 * x - 17)

def f(x):

return(x ** 4 + 7 * x ** 3 + 5 * x ** 2 - 17 * x + 3)

#Gradient of f

def g(x):

return(4 * x ** 3 + 21 * x ** 2 + 10 * x - 17)

در گام بعد نقاط اولیه شروع الگوریتم را تعریف کردم. با توجه به آنکه تضمینی نیست که حتماً الگوریتم از یک نقطه شروع اولیه به کمینه مطلق آن همگرا شود، من به‌صورت تصادفی ۱۰ نقطه اولیه را در بازه ۶- تا ۲+ انتخاب کردم و برای همه آن‌ها الگوریتم گرادیان کاهشی را پیاده‌سازی می‌کنم.

#Random initialization of x
import numpy as np
np.random.seed(123)
x = np.random.uniform(-6, 2, 10)
x

array([-0.42824652, -3.71088532, -4.18518837, -1.58948185, -0.24424824,
       -2.61514832,  1.84611359, -0.52136209, -2.15254479, -2.86305985])

#Random initialization of x

import numpy as np

np.random.seed(123)

x = np.random.uniform(-6, 2, 10)

array([-0.42824652, -3.71088532, -4.18518837, -1.58948185, -0.24424824,

-2.61514832, 1.84611359, -0.52136209, -2.15254479, -2.86305985])

سپس تابع گرادیان کاهشی را بر اساس رابطه ریاضی که در بالا آورده‌ام، نوشتم:

#Gradient Descent Function
#x_i+1 = x_i - gamma * g(x_i)
def grad_descent(x, gamma = 0.01, iter = 100):
    all_x = [x]
    for i in range(iter):
        x = x - gamma * g(x)
        all_x.append(x)
    return(all_x[-1])

#Gradient Descent Function

#x_i+1 = x_i - gamma * g(x_i)

def grad_descent(x, gamma = 0.01, iter = 100):

all_x = [x]

for i in range(iter):

x = x - gamma * g(x)

all_x.append(x)

return(all_x[-1])

این تابع نقطه اولیه، نرخ یادگیری و تعداد تکرار الگوریتم را دریافت می‌کند آخرین عددی را که الگوریتم گرادیان کاهشی به آن رسیده به‌عنوان خروجی نهایی برمی‌گرداند. درنهایت تابع را برای ۱۰ نقطه اولیه، با نرخ یادگیری ۰٫۰۱ و تکرار ۱۰۰ اجرا می‌کنم.

res = grad_descent(x, gamma = 0.01, iter = 100)
res

array([ 0.66238088, -4.48026848, -4.48026848, -4.48026848,  0.66238088,
       -4.48026848,  0.66238088,  0.66238088, -4.48026848, -4.48026848])

res = grad_descent(x, gamma = 0.01, iter = 100)

res

array([ 0.66238088, -4.48026848, -4.48026848, -4.48026848, 0.66238088,

-4.48026848, 0.66238088, 0.66238088, -4.48026848, -4.48026848])

همان‌طور که مشخص است نتایج این ۱۰ نقطه ما را به دو $x$ برای کمینه نسبی تابع رساند. برای آنکه بفهمیم کدام نقطه کمینه مطلق است کافی است مقدار $f$ را محاسبه کنیم. به‌این‌ترتیب مشخص می‌شود کمینه مطلق تابع $f$ نقطه $x = -4.48$ و $f(x) = -47.07$ است.

f(res)

array([ -3.83990263, -47.0747901 , -47.0747901 , -47.0747901 ,
        -3.83990263, -47.0747901 ,  -3.83990263,  -3.83990263,
       -47.0747901 , -47.0747901 ])

f(res)

array([ -3.83990263, -47.0747901 , -47.0747901 , -47.0747901 ,

-3.83990263, -47.0747901 , -3.83990263, -3.83990263,

-47.0747901 , -47.0747901 ])

می‌توانیم نقاط کمینه به‌دست‌آمده را بر روی تصویر تابع بیندازیم تا از صحت نتایج مطمئن شویم (شکل-۸).

#Plot f(x) and local minima
import matplotlib.pyplot as plt
x = np.arange(-6, 2, 0.01)
y = f(x)
plt.plot(x, y, color = 'red')
plt.plot(res[0], f(res[0]), color = 'blue', marker = 'o') #frist minimum
plt.plot(res[1], f(res[1]), color = 'blue', marker = 'o') #second minimum
plt.grid()

#Plot f(x) and local minima

import matplotlib.pyplot as plt

x = np.arange(-6, 2, 0.01)

y = f(x)

plt.plot(x, y, color = 'red')

plt.plot(res[0], f(res[0]), color = 'blue', marker = 'o') #frist minimum

plt.plot(res[1], f(res[1]), color = 'blue', marker = 'o') #second minimum

plt.grid()

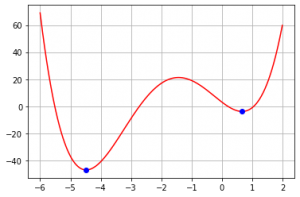
شکل-۸

منابع:

Deisenroth, M. P., Faisal, A. A., & Ong, C. S. (2020). “Mathematics for Machine Learning”, Cambridge University Press

آنالیکا

الگوریتم گرادیان کاهشی چیست؟

درک شهودی از الگوریتم گرادیان کاهشی

الگوریتم گرادیان کاهشی برای توابع چندمتغیره

پیاده‌سازی الگوریتم گرادیان کاهشی در پایتون

دیدگاهتان را بنویسید لغو پاسخ