رگرسیون خطی به زبان ساده برای مدیران

یکی از مهم‌ترین روش‌های تحلیل داده در کسب‌وکار، رگرسیون خطی (Linear Regression) است. رگرسیون خطی، یکی از مهمترین الگوریتم‌های یادگیری ماشین هم هست. اگرچه در بیشتر موارد مدیران خود چنین تحلیل‌هایی را انجام نمی‌دهند، برای تصمیم‌گیری بر مبنای خروجی‌های تحلیل رگرسیون نیاز است تا با مفاهیم آن آشنا باشند. من در این مقاله به معرفی تحلیل رگرسیون می‌پردازم.

تحلیل رگرسیون چیست؟

فرض کنید شما مدیر بازاریابی یک خرده‌فروشی زنجیره‌ای هستید و علاقه‌مندید میزان فروش ماه آینده کالایی را پیش‌بینی کنید. شما می‌دانید که صدها عامل مانند وضعیت آب‌وهوا تا برنامه‌های ترویجی رقبا بر روی میزان تقاضای آن کالا اثر می‌گذارد. برخی از همکاران شما هم حدس‌های خود را دارند. برای مثال یکی از آن‌ها اصرار دارد که در ماه‌های بارانی میزان فروش آن محصول بالا می‌رود. دیگری می‌گوید به تجربه فهمیده که پس از گذشت چهار هفته از زمانی که خرده‌فروش رقیب تخفیف‌های ویژه می‌گذارد، فروش آن کالا رشد چشم‌گیری می‌کند.

این‌ها همه فرضیاتی هستند که باید آزمایش شوند. تحلیل رگرسیون یک روش ریاضی است که به ما کمک می‌کند بفهمیم کدام‌یک از این عوامل در واقعیت مؤثر هستند. تحلیل رگرسیون به پرسش‌هایی مانند زیر پاسخ می‌دهد:

کدام عوامل مهم‌ترین اثر را دارند؟

از کدام‌یک می‌توان صرف‌نظر کرد؟

اثر متقابل این عوامل چگونه است؟

چقدر از میزان اثرگذاری این عوامل مطمئن هستیم؟

در تحلیل رگرسیون این عوامل “متغیر” نامیده می‌شوند. متغیر وابسته عاملی است که می‌خواهیم پیش‌بینی کنیم. در مثال خرده‌فروشی میزان فروش ماهیانه کالا متغیر وابسته است. عواملی که حدس می‌زنیم بر روی متغیر وابسته اثر می‌گذارند، متغیرهای مستقل نامیده می‌شوند.

چگونه تحلیل رگرسیون خطی انجام می‌شود؟

برای انجام تحلیل رگرسیون به‌عنوان یکی از روش‌های داده‌کاوی (Data Mining) باید از یک سری گام‌های کلی پیروی کرد که من در مقاله دیگری درباره فرآیند انجام پروژه‌های داده‌کاوی توضیح داده‌ام. در اینجا تنها روی تحلیل داده‌ها متمرکز می‌شوم.

طبیعتاً برای تحلیل رگرسیون خطی لازم است تا در مورد متغیرهای موردنظر داده جمع‌آوری کرد. در مثال گفته‌شده، لازم است تا داده‌های میزان فروش ماهیانه در چند سال گذشته استخراج شود. فرض کنید اثر بارندگی را بر روی میزان فروش می‌خواهیم بسنجیم. به‌این‌ترتیب باید داده‌های میزان بارش متوسط ماهیانه در منطقه را برای همان دوره زمانی استخراج کرد. فرض کنید نمودار پراکندگی این داده‌ها را رسم کردیم و مانند شکل-۱ شده است.

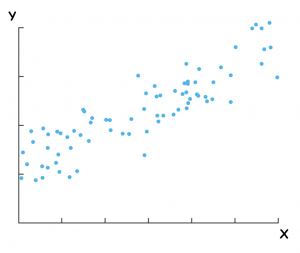
در شکل-۱ محور عمودی نشان‌دهنده متغیر وابسته (میزان فروش ماهیانه) و محور افقی نشان‌دهنده متغیر مستقل (میزان بارش متوسط ماهیانه) است. با نگاه کردن به شکل-۱ این دیدگاه تقویت می‌شود که در ماه‌های پربارش میزان فروش افزایش می‌یابد. گرچه این موضوع جالب است ولی میزان اثرگذاری بارش بر روی فروش چقدر است؟ برای مثال اگر در ماهی بارش متوسط ۱۵ میلی‌متر باشد، چه برآوردی از میزان فروش می‌توان داشت؟ اگر میزان بارش ۳۰ میلی‌متر باشد چطور؟

حال تصور کنید از نمودار شکل-۱ خطی را عبور دهیم که به‌طور تقریبی از میان همه نقاط عبور کند. این خط به ما کمک می‌کند تا با حدی از قطعیت، تخمین بزنیم وقتی میزان مشخصی از بارش داشته باشیم، میزان فروش چقدر خواهد بود. این خط، خط رگرسیون نامیده می‌شود (شکل-۲). با استفاده از نرم‌افزارهایی مانند اکسل (Excel) یا R می‌توان به‌راحتی این خط را رسم کرد. خط رگرسیون بهترین خطی است که می‌توان از داده‌ها عبور داد. به‌عبارت‌دیگر این خط بهترین خطی است که رابطه بین متغیر وابسته و متغیر مستقل را توضیح می‌دهد. علاوه بر نمایش این خط، می‌توان معادله آن را نیز به دست آورد.

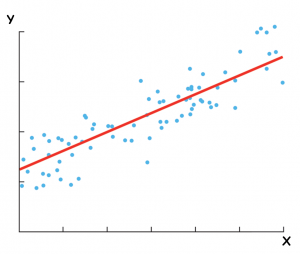
فرض کنید معادله خط رگرسیون در شکل-۲ از رابطه زیر به دست آید:

فرمول بالا رابطه بین میزان بارش () و میزان فروش را بیان می‌کند. همچنین  بیانگر میزان خطا در برآورد است. اگر آن را نادیده بگیریم، رابطه بالا به شکل زیر درمی‌آید:

بر این اساس اگر هیچ بارشی نداشته باشیم، انتظار می‌رود فروش ماهیانه ۱۵۰ واحد باشد. این جمله بدان معنی است که بر اساس داده‌های تاریخی در ماه‌هایی که بارشی نداشتیم، میانگین میزان فروش ۱۵۰ واحد بوده است و اگر روند گذشته تکرار شود این میزان فروش مورد انتظار خواهد بود. ضریب متغیر بیان می‌کند به ازای هر میلی‌متر افزایش بارش به‌طور متوسط ۲٫۵ واحد به فروش اضافه می‌شود.

اما درستی چنین نتیجه‌گیری به میزان خطا بستگی دارد. خط رگرسیون همواره با خطا همراه است. در دنیای واقعی متغیر مستقل هیچ‌گاه پیش‌بینی کننده دقیق متغیر وابسته نیست. درواقع با استفاده از داده‌های جمع‌آوری‌شده این خط یک برآورد از رابطه است. میزان خطا به ما می‌گوید تا چه حد به این برآورد مطمئن هستیم. هرچه میزان خطا بیشتر باشد، اطمینان ما به خط رگرسیون کاهش می‌یابد.

در این مثال تنها یک متغیر مستقل (میزان بارش) در معادله در نظر گرفته شد. معمولاً در تحلیل‌های رگرسیون ما علاقه‌مند هستیم تا اثر چندین متغیر مستقل را بدانیم. اضافه کردن متغیرهای مستقل دیگر مانند اثر برنامه‌های ترویجی رقبا می‌تواند خطای مدل را کاهش دهد، اگرچه اضافه کردن متغیرهای زیاد هم مسائل خود را دارد که خارج از بحث این مقاله است. یکی از مزایای مهم رگرسیون آن است که شما می‌توانید به‌طور هم‌زمان اثر متغیرهای مختلف را بر روی متغیر وابسته سنجش کنید. از این تکنیک به‌عنوان رگرسیون چند متغیره (Multiple Regression) نام برده می‌شود.

چگونه مدیران کسب‌وکارها می‌توانند از تحلیل رگرسیون خطی استفاده کنند؟

بسیاری از تصمیمات مدیریتی بر اساس روابطی که تصمیم‌گیر بین چند متغیر فرض می‌کند بنا می‌شود. برای مثال اگر مدیر بر این باور باشد که میزان تبلیغات بر روی میزان فروش مؤثر است، به‌منظور افزایش فروش میزان تبلیغات را افزایش می‌دهد. در برخی موارد مدیران تنها بر روی شهود خود متکی هستند تا این روابط را شناسایی کنند. اما روش‌های شهودی تحت تأثیر خطاهای رفتاری هستند. در مقابل در تصمیم‌گیری داده‌محور، تصمیم‌گیر با تکیه‌بر شواهد، مبتنی برداده و بهره‌گیری از روش‌های آماری به قضاوت نهایی می‌رسد. تحلیل رگرسیون یکی از روش‌های مهم و پرکاربردی است که مدیران می‌توانند از آن استفاده کنند تا روابط بین متغیرهای درگیر در مسئله را به شکل کمّی دربیاورند و تبیین کنند.

موردکاوی در حوزه بازاریابی و فروش

در اینجا به‌اختصار به یک موردکاوی در حوزه بازاریابی و فروش می‌پردازم. یک شرکت تولیدی در حوزه مواد غذایی و خوراکی در آستانه عرضه محصول جدیدش با عنوان “شوکوهایپ” است. شوکوهایپ یک نوع شکلات انرژی‌زاست. اگرچه بازار شکلات‌های انرژی‌زا در ابتدا به ورزشکاران حرفه‌ای مانند کوهنوردان و دوچرخه‌سواران محدود می‌شد اما با محبوب شدن تناسب‌اندام و بدن‌سازی بین عموم مردم مصرف این نوع شکلات‌ها که کالری مناسبی دارند و با ویتامین و پروتئین غنی شده‌اند، طرفدار پیدا کرده است. این بازار هنوز در ابتدای راه خود است و گرچه چند محصول مشابه نیز در بازار وجود دارند ولی شرکت به دنبال آن است تا با یک کمپین تبلیغاتی قدرتمند سهم زیادی از بازار را به خود اختصاص دهد.

این شرکت با رویکرد تصمیم‌گیری داده‌محور آشناست. آنان به‌منظور کاهش ریسک، قبل از عرضه این محصول در سطح گسترده، سعی می‌کنند این ایده را در بازار آزمایش کنند. به همین دلیل شش ماهی است که شوکوهایپ را  به‌صورت آزمایشی در دو شهر کرج و مشهد عرضه کردند. هدف آن است تا به‌زودی محصول را در بازار اصلی یعنی تهران عرضه کنند.

لازم به ذکر است در دوره آزمایشی این محصول با قیمت‌های متفاوت عرضه شد تا واکنش مصرف‌کنندگان نسبت به قیمت سنجیده شود. همین‌طور به‌منظور افزایش آگاهی مشتریان از محصول جدید روش‌های ترویجی درون فروشگاهی مانند پوسترهای تبلیغاتی و ارائه کوپن‌های تخفیف استفاده شد. داده‌های فروش ۳۴ فروشگاه در دوره آزمایشی جمع‌آوری شده‌اند. این داده‌ها شامل تعداد فروش در هر فروشگاه، قیمت عرضه، هزینه تبلیغات درون فروشگاهی، محل عرضه محصول در قفسه فروشگاه (جایگاه‌های ویژه جداگانه‌ در مقابل قفسه‌های معمولی درون فروشگاهی) و وجود یا عدم وجود دستگاه توزیع کوپن تخفیف در فروشگاه است.

تحلیل رگرسیون نشان داد وجود یا عدم وجود دستگاه توزیع کوپن تخفیف تأثیری بر میزان فروش ندارد. در مقابل قیمت، هزینه تبلیغات درون فروشگاهی و محل عرضه عوامل مؤثر بر میزان فروش هستند. معادله رگرسیون برای این داده‌ها به شکل زیر است:

توجه کنید این رابطه یک رگرسیون چند متغیره است چراکه به‌طور هم‌زمان اثر چندین متغیر مستقل بر روی متغیر وابسته مشخص شده است. این رابطه رگرسیون می‌تواند به تصمیم‌گیری‌های کلیدی در زمان عرضه گسترده محصول کمک کند.

اول، با بهره‌گیری از این رابطه رگرسیون، می‌توان تحلیل حساسیت تقاضا نسبت به قیمت را انجام داد. ضریب متغیر  در رابطه رگرسیون می‌گوید هر واحد افزایش قیمت، تقریباً ۰٫۷ واحد از میزان تقاضا می‌کاهد (به‌طور متوسط هر ۱۰۰ تومان افزایش قیمت ۷۰ واحد از تقاضا می‌کاهد). همچنین حال که رابطه قیمت با تقاضا روشن شده است با جایگذاری در رابطه زیر، می‌توان قیمت بهینه را که در آن سود بیشینه می‌شود، مشخص کرد.

دوم، با توجه به بودجه محدود بازاریابی که قرار است صرف فعالیت‌های ترویجی در هر فروشگاه شود، می‌توان میزان کارایی روش‌های مختلف را مشخص کرد. همان‌طور که مشخص شد استفاده از کوپن‌های تخفیف کارایی چندانی نداشته است. ضرایب رگرسیون کمک می‌کند تا اثر تبلیغات پوستری درون فروشگاهی و عرضه محصول در جایگاه‌های ویژه جداگانه بر روی افزایش فروش مشخص شود. برای مثال رابطه رگرسیون نشان می‌دهد که عرضه محصول در جایگاه‌های ویژه جداگانه میزان فروش را ۷۷۱ واحد افزایش می‌دهد (توجه شود متغیر یک متغیر دودویی است و مقدار ۰ یا ۱ می‌گیرد؛ صفر به معنی عرضه در قفسه‌های معمولی و یک به معنی عرضه در جایگاه‌های ویژه). با داشتن هزینه‌های هر روش تبلیغاتی می‌توان تحلیل فایده-هزینه (Benefit/Cost Analysis) نیز انجام داد.

سوم، با دانستن این رابطه امکان پیش‌بینی اثر هم‌زمان سناریوهای مختلف قیمت‌گذاری و تخصیص بودجه به روش‌های مختلف تبلیغاتی به وجود می‌آید.

در تحلیل رگرسیون خطی باید به چه نکاتی توجه کرد؟

در استفاده از رگرسیون خطی باید توجه کرد که همبستگی (Correlation) با علّیت (Causation) تفاوت دارد. در مقاله “چرا مدیران باید تفاوت بین همبستگی و رابطه علّی را بدانند؟” به‌طور مفصل با ارائه نمونه‌هایی توضیح داده‌ام که چرا این نکته اهمیت دارد. به‌طور خلاصه هم‌زمانی دو پدیده لزوماً به این معنی نیست که یکی عامل دیگری است.

این‌که داده‌ها نشان می‌دهد بین آمدن باران و فروش محصول رابطه وجود دارد، دلیلی بر این نیست که آمدن باران دلیل افزایش فروش محصول می‌شود. در اینجا لازم است یک رابطه منطقی بین دو متغیر وجود داشته باشد. وجود رابطه علّیت با مطالعات میدانی یا قضاوت فردی است که باید مشخص شود. اگر منطقاً بتوان دو متغیر را به یکدیگر مربوط فرض کرد و با استفاده از رگرسیون خطی یا سایر روش‌های آماری این رابطه تائید شود، می‌توان به نتایج اعتماد کرد. در مقاله دیگری توضیح دادم چه زمانی می‌توان بر اساس همبستگی عمل کرد.

در مقاله “چگونه رابطه علّی را تشخیص دهیم؟” به سه معیاری می‌پردازم که با توجه به آن‌ها وجود رابطه علّی را می‌توانید تشخیص دهید.

مانند هر پروژه داده‌کاوی دیگر، همراهی و همکاری کسانی که شهود خوبی نسبت به کسب‌وکار دارند با کسانی که مدل‌سازی‌های آماری انجام می‌دهند ضروری است. مدیر نباید کارشناس داده‌کاوی را به حال خود رها کند تا در داده‌ها به دنبال روابط بگردد. مدیر به همراه کارشناس داده‌کاوی فرضیاتی را مطرح می‌کند و با استفاده از داده درستی یا نادرستی آن فرضیات بررسی می‌گردد. اگر دانشمند داده بدون هیچ فرضیه‌سازی به دنبال روابط درون داده‌ها بگردد، بالاخره روابطی پیدا خواهد کرد؛ روابطی که ممکن است تنها براثر تصادف در داده‌ها ایجاد شده‌اند و در دنیای واقعی مصداقی ندارند. مثل این می‌ماند که آن‌قدر سکه بیندازید تا احساس کنید الگوی جالبی در پرتاب سکه‌ها پیدا کردید؛ برای مثال چند بار پشت سرهم خط بیاید. درحالی‌که این الگو تنها در اثر شانس بوده است.

نکته دیگر مربوط به خطا در میزان برآورد () است. اگر رگرسیون را روی هر مجموعه از داده‌هایی امتحان کنید، حتماً یک معادله ریاضی به دست می‌آورید. اما این بدان معنی نیست که لزوماً آن رابطه ریاضی در دنیای واقعی بین متغیرها برقرار است. همیشه رابطه به دست آمده با عدم قطعیت همراه است. اگر تحلیل رگرسیون خطی نشان دهد که ۹۰ درصد تغییرات متغیر وابسته توسط آن رابطه توضیح داده می‌شود این خبر خوبی است. ولی اگر رابطه رگرسیون تنها ۱۰ درصد تغییرات را توضیح می‌دهد، رابطه قوی بین متغیرها برقرار نیست. به عبارتی رگرسیون کمک می‌کند میزان قطعیت در پیش‌بینی را مشخص کنید. درواقع رگرسیون نمی‌گوید چگونه بارندگی روی فروش اثر می‌گذارد بلکه می‌گوید با چه احتمالی بارندگی روی فروش مؤثر است.

 نکته آخر این‌که مدیر باید در فرآیند مدل‌سازی نقش فعال داشته باشد. شهود مدیران باید همراه مدل‌های ریاضی باشد و قرار نیست جایگزین آن شود. همچنین اگر نتیجه‌ای با شهود شما هم‌خوانی ندارد بلافاصله نتایج را رد نکنید. بلکه به دنبال بررسی و تحلیل بیشتر در دنیای واقعی باشید.

برای آشنایی بیشتر با نحوه فکر کردن به مسائل دنیای واقعی مبتنی بر رویکرد داده-محور مقاله “چگونه مانند یک دانشمند داده فکر کنید؟ راهنمایی برای مدیران اجرایی” را مطالعه کنید.

منابع:

Camm, D.C., Cochran, J.J., Fry, M.J., Ohlmann, J.W., Anderson, D. R., Sweeney, D.J., Williams, T.A. (2015). “Essentials of Business Analytics”, Cengage Learning

Harvard Business Review (2017). “HBR Guide to Data Analytics Basics for Managers”, Harvard Business Review Press, Boston, Massachusett