
امروزه رمزنگاری (Cryptography) در قلب ارتباطات مبتنی بر اینترنت، تجارت الکترونیک (E-commerce)، پرداختهای بانکی و محصولات مبتنی بر فنآوری زنجیره بلوک (Blockchain) مانند بیتکوین (Bitcoin) قرار دارد. به همین دلیل مدیران لازم دارند تا برای فهم دقیق این فنآوریها با مفاهیم اولیه رمزنگاری آشنا باشند. در این مقاله من به مرور تاریخچه رمزنگاری و اصول اولیه آن خواهم پرداخت. گرچه امروزه رمزنگاری کاملاً مبتنی بر الگوریتمهای ریاضی است، من در این مقاله سعی کردم مفاهیم رمزنگاری را به زبان ساده و قابلفهم توضیح دهم بهگونهای که پیشنیاز زیادی ازنظر دانش ریاضی برای فهم آن وجود نداشته باشد.
مروری بر تاریخ رمزنگاری
از همان ابتدا که زبان پدید آمده، تلاشها برای مخفی نگهداشتن پیامها نیز در جریان بوده است. در تاریخ ایران یکی از اولین موارد در این خصوص به داستان به قدرت رسیدن کورش اولین پادشاه هخامنشی برمیگردد. نقل شده است هارپاگ، از نزدیکان پادشاه ماد که از او کینه به دل داشت، برای ارسال نامه به کوروش و تشویق او به سرنگونی پادشاه، پیامش را در شکم خرگوشی گذاشته، باظرافت شکم خرگوش را دوخته و به یکی از خدمتکاران وفادار خود گفته بود که لباس شکارچیان را بپوشد و نامه را پنهانی به کوروش برساند.
اما بهجز روش فیزیکی برای پنهان کردن پیام مانند آنچه هارپاگ انجام داد، انسانها به دنبال این بودند تا پیام را به شکلی منتقل کنند که اگر توسط شخص سوم (شنودکننده پیام) کشف شد، نتواند به محتوای آن پی ببرد. رمزنگاری هنر پنهان کردن پیام از شنودکننده با بهرهگیری از رمزی است که تنها طرفین ارتباط از آن آگاهاند. گرچه این تعریف شاید همه کاربردهای امروزی رمزنگاری را پوشش ندهد، برای شروع بحث مفید است.
برای نمونه در دوره ساسانی، ایرانیان هفت زبان داشتند. شاه دبیره برای مراسلات رسمی بکار میرفته و برای مردم عادی ممنوع بوده است. راز سَهریه زبان دیگری بوده که برای ارسال و یا دریافت پیامهای محرمانه به سران کشورهای خارجی استفاده میشده است.
یکی از رایجترین نمونههای ابتدایی رمزنگاری، کد سزار (Caesar Cipher) نام دارد. ژولیوس سزار (Julius Caesar) برای مکاتبه با فرماندهان خود هر حرف در متن اصلی را با حرف دیگری با فاصله ثابت جابجا میکرد. بهاینترتیب نامهها در صورت کشف بیمعنی به نظر میرسیدند. فرض کنید فرد الف و ب میخواهند با کد سزار با یکدیگر پیام مبادله کنند. پیش از هر چیز آنان باید بر سر میزان جابجایی حروف باهم توافق کنند. فرض کنید آنان توافق کردند هر حرف را با سه حرف جلوتر از خود جانشین کنند (شکل-۱). بهاینترتیب پیامی مانند “زمان ملاقات هشت شب فردا” به شکل “ش ه ت ی ه و ت ل ت چ ب ط چ ط ث گ س ز ت” رمزنگاری میشود. فرد ب برای رمزگشایی بهراحتی حروف را بهاندازه سه واحد جابجا و پیام اصلی را آشکار میکند. این روش برای صدها سال پس از سزار استفاده شد.

نقطهضعف این روش ۸۰۰ سال بعد توسط ابویوسف الکندی (Al-Kindi)، فیلسوف و ریاضیدان عرب، در مقالهای منتشر شد. او کد سزار را بر اساس یکی از مهمترین ویژگیهای زبان شکست. اگر شما نوشتههای یک زبان را تحلیل آماری کنید و فراوانی حروف را در نوشتهها به دست آورید، یک الگوی پایدار مشاهده خواهید کرد. من این کار را برای زبان فارسی انجام دادم (بخش اول ضمیمه مقاله را مطالعه کنید). شکل-۲، فراوانی حروف فارسی در نوشتهها را نشان میدهد.

همانطور که میبینید حروف با فرکانسهای مختلفی در متون فارسی استفاده میشوند. هنگامیکه از زبان فارسی یا هر زبان دیگر برای انتقال پیام استفاده میکنیم، بهطور ناخودآگاه سرنخی را برای شنودکننده بهجای میگذاریم. وقتی فرد الف و ب بارها و بارها از کد سزار برای انتقال پیام استفاده یا یک متن نسبتاً طولانی را ردوبدل میکنند، سرنخ شروع بهظاهر شدن میکند. تحلیل فراوانی حروف بهکاررفته در متن رمزنگاریشده و مقایسه آن با فراوانی حروف در زبان فارسی میزان جابجایی کلمات در کد سزار را برملا میکند. برای مثال اگر حرف ت در پیام رمزنگاریشده بیشترین فراوانی را دارد، از آنجا که بیشترین فراوانی در زبان فارسی به حرف الف تعلق دارد با احتمال زیاد میزان جابجایی ۳ است. به این روش تحلیل فراوانی (Frequency Analysis) در شکستن رمز گفته میشود.
برای اینکه در یک متن توزیع فراوانی حروف یکنواختتر و بنابراین شکستن کد دشوارتر شود، روش رمزنگاری چندحرفی (Polyalphabetic Cipher) ابداع شد. این بار تصور کنید فرد الف و ب بر روی یک کلمه رمز برای مشخص کردن میزان جابجایی حروف توافق کردند. برفرض این کلمه “جهان” باشد. فرد الف برای رمزنگاری پیام خود، حروف این کلمه را بر اساس رتبه حروف در الفبا به عدد تبدیل میکند (شکل-۳). سپس این زنجیره اعداد را در طول نامه تا انتها تکرار میکند و هر حرف پیام را بهاندازه عدد متناظر آن جابجا میکند (شکل-۳). بهاینترتیب فرد الف بجای یک جابجایی، چندین جابجایی را در پیام استفاده میکند. فرد ب برای باز کردن پیام برعکس همین روند را انجام میدهد.
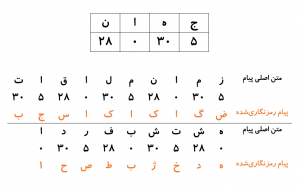
حال اگر فرد ج بهطور متوالی پیامهای تبادلشده را شنود کند، مشاهده خواهد کرد که حروف بهطور یکنواختتری در پیامهای رمزنگاریشده توزیع شدهاند. ولی همچنان تکرار، سرنخ را به شنودکننده میدهد. اگر متن بهاندازه کافی بلند باشد، برخی از کلمات پرتکرار ممکن است چندین بار با کلمه رمز همردیف شوند. این موجب میشود که در پیام رمزنگاریشده دنبالهای از حروف تکرار شوند. این میتواند سرنخی از تعداد حروف کلمه رمز دهد. فرض کنید، فرد ج متوجه شد که کلمه رمز چهارحرفی است. بهاینترتیب روی هر چهار حرف یکبار، سه حرف یکبار و الیآخر تحلیل فراوانی انجام میدهد.
برای نمونه شکل-۴ پیام محرمانهای است که آلمان در جنگ جهانی اول برای مکزیک با روش رمزنگاری چندحرفی فرستاده است. این پیام توسط انگلستان شکسته شد و نقش مهمی در تغییر سرنوشت جنگ جهانی اول بازی کرد. برای سرگرمی میتوانید سعی کنید، پیام را بشکنید.
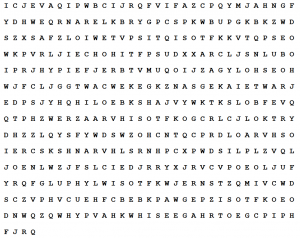
پاسخ را در فایل زیر مشاهده کنید.
Zimmerman Telegram from Germany to Mexico
اهمیت فرآیندهای تصادفی در رمزنگاری
کلاود شانون (Claude Shannon)، بنیانگذار تئوری اطلاعات، محرمانگی ایدئال (Perfect Secrecy) را اینگونه تعریف میکند که اگر یک پیام ردیابی شود احتمال شکستن رمز پیام پس از ردیابی با احتمال شکستن آن قبل از ردیابی هیچ تفاوتی نکند.
برای سالها پرسش این بود که چگونه میتوان بهطور کامل سرنخها را در پیامهای رمزنگاریشده از بین برد. پاسخ در فرآیندهای تصادفی است. فرض کنید فرد الف برای تولید میزان جابجایی حروف، یک تاس ۳۲ وجهی میاندازد و میزان جابجایی هر حرف را بر اساس آن تعیین میکند. مهم است که این کار را به تعداد حروف پیام انجام دهد. بهاینترتیب یک کلید رمز بلند که کاملاً تصادفی تولیدشده ایجاد میگردد. در این حالت شنودکننده پیام دچار مشکل میشود چراکه روش رمزنگاری دو ویژگی مهم دارد. اول، چون برای هر حرف میزان جابجایی به شکل تصادفی (با توزیع احتمال یکسان) بهدستآمده، هیچ الگوی تکرارشوندهای در متن رمزگذاری شده یافت نخواهد شد. دوم، وقتی فرد ج پیامهای ردوبدل شده را تحلیل فراوانی میکند با یک نمودار فراوانی کاملاً یکنواخت مواجه میشود. بهاینترتیب برای فرد ج ناممکن میشود که آن را با توزیع فراوانی واقعی حروف مقایسه کند.
برای فهمیدن قدرت این روش، یک کلمه پنج حرفی را در زبان فارسی در نظر بگیرید. اگر با روش سزار آن را رمزنگاری کنیم، ۳۲ حالت ممکن برای میزان جابجایی وجود دارد. بهاینترتیب با این روش یک کلمه پنجحرفی را به ۳۲ حالت ممکن میتوان رمزگذاری کرد. تعداد زیادی حالت وجود ندارد و میتوان همه آنها را آزمود. اما در روشی که هر حرف به شکل تصادفی جابجا میشود، ۳۲ به توان ۵ حالت ممکن برای رمزنگاری یک کلمه پنجحرفی وجود دارد؛ برابر تقریباً ۳۳ میلیون حالت مختلف که همگی با احتمال یکسان ممکن است معادل پیام اصلی باشند.
امروزه الگوریتمهای ریاضی رمزنگاری مبتنی بر تولید عدد تصادفی هستند. اگر به پدیدههای طبیعی اطراف خود نگاه کنیم میتوان فرآیندهای تصادفی بسیاری دید. اگر بتوان این پدیدهها را در هرلحظه اندازهگیری کرد، زنجیره اعداد تولیدشده کاملاً تصادفی است. برای مثال ذرات دود به شکل کاملاً تصادفی در هوا پخش میشوند. در هرلحظه حرکت بعدی ذره دود را نمیتوان پیشبینی کرد (شکل-۵).

اما تولید عدد تصادفی برای انسان با استفاده از ماشین ساده نیست. ماشینها قابل پیشبینی هستند و الگوهای تکرارشونده در رفتار آنان وجود دارد. همین عدم قابلیت تولید اعداد کاملاً تصادفی موجب شد که دستگاه رمزنگاری انیگما (Enigma Machine) در جنگ جهانی دوم شکسته شود. انیگما یک دستگاه الکترومکانیکی بود که آلمانها در جنگ جهانی دوم از آن برای مبادله پیام بین واحدهای نظامی خود استفاده میکردند. انیگما در ظاهر مانند یک دستگاه تایپ معمولی بود (شکل-۶). برای تبادل پیام، ارسالکننده و گیرنده هردو باید دستگاه را میداشتند. انیگما با این هدف طراحی شده بود که حتی اگر شنودکننده به آن دسترسی پیدا کند و از ساختار داخلی آن مطلع شود، نتواند کد پیامهایی را که با آن رمزگذاری میشود، بشکند (نمونهای از محرمانگی ایدئال).

به شکل ساده این دستگاه حروف ورودی را میگرفت و هر یک را به شکل تصادفی جابجا میکرد. انیگما دارای چرخهای گردانندهای بود که موقعیت آنها نسبت به هم کلید رمز را مشخص میکرد. کلید رمز پس از زمانهای کوتاهی تغییر داده میشد. بر اساس کلید رمز، انیگما حروف ورودی را به حروف دیگری تبدیل و پیام را رمزگذاری میکرد. گرچه آلمانها تمامی سعی خود را کرده بودند تا حروف به شکل تصادفی جابجا شود، خطاهایی کوچک در طراحی موجب شد، این فرآیند آنچنان هم که آنان تصور میکردند تصادفی نباشد. آلن تورینگ (Alan Turing)، دانشمند انگلیسی و از بنیانگذاران علم محاسبهٔ نوین و هوش مصنوعی (Artificial Intelligence)، نقش مهمی در شکستن کدهای انیگما داشت. فعالیتهای تورینگ در این پروژه کمکهای زیادی به توسعه کامپیوترهای امروزی و حوزه هوش مصنوعی کرد.
مولدهای اعداد شبه تصادفی
در کامپیوترهای امروزی از مولد اعداد شبه تصادفی (Pseudo Random Number Generator) استفاده میشود. جان فون نویمن (John von Neumann)، ریاضیدان آمریکایی، یک روش بسیار ساده برای تولید اعداد تصادفی ارائه کرد. برای انجام این روش او پیشنهاد کرد ابتدا یک عدد کاملاً تصادفی انتخاب کنیم. این عدد میتواند از اندازهگیری یک پدیده تصادفی در طبیعت به دست آید که به آن مقدار اولیه (Seed) گفته میشود. مقدار اولیه در سادهترین شکل میتواند زمان فعلی بر اساس میلیثانیه باشد. سپس این عدد اولیه را در خودش ضرب کنیم. سپس ارقام میانی را انتخاب کنیم. این عدد را بهعنوان مقدار اولیه برای محاسبه بعدی در نظر بگیریم و فرآیند را ادامه دهیم (شکل-۷).

این روش یکی از ابتداییترین الگوریتمهای تولید عدد تصادفی است. میزان تصادفی بودن رشته اعداد تنها به تصادفی بودن عدد اولیه بستگی دارد. برای مقدار اولیه یکسان، خروجی همواره یکی است.
اما چه تفاوتی بین این رشته از اعداد شبهتصادفی با اعداد کاملاً تصادفی وجود دارد؟ در شکل-۸ من تفاوت این دو روش را بهطورگرافیکی نشان دادم. تصویر سمت چپ ناشی از یک فرآیند کاملاً تصادفی، درحالیکه تصویر سمت راست ناشی از یک فرآیند شبهتصادفی است. فرآیندهای شبهتصادفی پس از مدتی شروع به تکرار خودشان میکنند و الگوهایی را نشان میدهند. در الگوریتم فون نیومن پسازآنکه الگوریتم دوباره به یکی از مقدارهای اولیه خود برگردد، زنجیره اعداد تکرار میشوند. اینکه پس از چه مدتی الگوریتم دوباره خود را تکرار میکند به طول ارقام مقدار اولیه برمیگردد. در حالتی که یک عدد دورقمی برای الگوریتم فون نیومن انتخاب کنیم، زنجیره اعداد در بهترین حالت پس از ۱۰۰ بار، تکرار میشوند. هرچه مقدار اولیه بزرگتر باشد، تکرار دیرتر رخ خواهد داد.

نکته دیگر در مورد فرآیندهای شبهتصادفی این است که آنان بهطور یکنواخت همه فضای اعداد را پوشش نمیدهند. فرض کنید حروف یک پیام ۲۰ حرفی به زبان فارسی را با یک فرآیند کاملاً تصادفی جابجا کردیم. در این حالت ۳۲ به توان ۲۰ حالت ممکن برای رمزنگاری چنین پیامی وجود دارد. برای اینکه احساسی نسبت به بزرگی این عدد داشته باشید، تصور کنید هر یک از این حالتها را روی یک برگه کاغذ بنویسم و آنها را رویهم بگذاریم. اگر شخصی در پایین کاغذها بایستد و نوری به سمت بالا بگیرد، نور پس از ۱۳ میلیارد سال به انتهای کاغذها خواهد رسید (با فرض ضخامت هر کاغذ ۰٫۱ میلیمتر). درحالیکه فرض کنید همین پیام را با الگوریتم فون نیومن با یک مقدار اولیه چهاررقمی رمزنگاری کنیم، چون ۹ هزار حالت ممکن برای مقدار اولیه داریم، تنها میتوانیم ۹ هزار زنجیره اعداد تصادفی متمایز تولید کنیم. بهاینترتیب فضای جواب در حالت شبهتصادفی بسیار بسیار کوچکتر از حالت تصادفی میشود.
بهطور خلاصه قسمت مهمی از الگوریتمهای رمزنگاری امروزی به این وابسته است که تا چه حد اعداد تولیدشده واقعاً تصادفی هستند. در حوزه کاربردی، مهم این است که زنجیره اعداد تولیدشده توسط الگوریتم به شکلی باشد که برای کامپیوتر مقدور نباشد در یکزمان قابلقبول تمامی حالتهای مقدار اولیه را بررسی کند. بهاینترتیب نمیتوان تفاوت بین حالت تصادفی و شبهتصادفی را تشخیص داد. این مسئله به اصل مهمی در رمزنگاری ختم میشود؛ تفاوت بین آن چیزی که ممکن است و آن چیزی که در یکزمان قابلقبول امکانپذیر است.
رمزنگاری متقارن و نامتقارن
شکل-۹ نمونهای از کلید رمزی است که در دوران قاجار برای مبادله پیام در ایران استفاده میشده است. این نمونه و تمامی مثالهایی که تا به اینجا اشاره کردم، از روش رمزنگاری متقارن (Symmetric Cryptography) بهره میبرند. در روش رمزنگاری متقارن، ارسالکننده و گیرنده پیام هر دو دارای یک کلید رمز برای رمزنگاری و رمزگشایی از پیام هستند. این کلید رمز باید از قبل از طریق یک کانال ایمن بهصورت فیزیکی منتقل شود. اما اگر طرفین یکدیگر را نشناسند و هیچ ارتباط قبلی باهم نداشته باشند چگونه در حضور شنودکننده، به یک کلید رمز مشترک برای رمزنگاری پیام برسند؟

در اواسط قرن بیستم با ورود به عصر دیجیتال و شبکههای کامپیوتری این پرسش اهمیت بسیاری پیدا کرد. تمام فعالیتهایی که در اینترنت انجام میشود مبتنی بر ارسال و دریافت پیام از یک سرور (Server) است. چگونه این پیامها رمزگذاری میشوند؟
در سال ۱۹۷۶، ویتفیلد دیفی (Whitfield Diffie) و مارتین هلمن (Martin Hellman) در مقالهای الگوریتمی ارائه کردند که مبنای رویکرد رمزنگاری نامتقارن (Asymmetric Cryptography) است. رمزنگاری نامتقارن به طرفین اجازه میدهد که یک کلید عمومی (Public Key) را با یکدیگر به اشتراک بگذارند تا پیام تنها توسط کسی که کلید خصوصی (Private Key) معادل آن کلید عمومی را دارد، رمزگشایی شود. به این روش، رمزنگاری کلید عمومی (Public Key Cryptography) نیز گفته میشود.
رمزنگاری کلید عمومی
فرض کنید فرد الف و ب یکدیگر را نمیشناسند و میخواهند بر سر یک کلید رمز سرّی توافق کنند. اما فرد ج دائماً در حال شنود پیام آنان است. چگونه این دو میتوانند بر سر یک کلید رمز مشترک توافق کنند؟
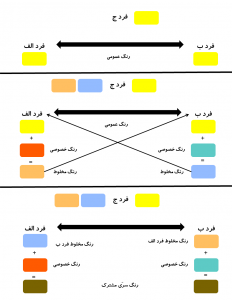
برای توضیح سادهتر مسئله، من از استعاره رنگها استفاده میکنم. بهاینترتیب پرسش بالا این میشود که چگونه فرد الف و ب بر سر یک رنگ سرّی مشترک توافق کنند. روش کلید عمومی مبتنی بر دو اصل است. اول، مخلوط کردن دو رنگ برای رسیدن به رنگ سوم همواره کار سادهای است. دوم، با داشتن یک رنگ مخلوط شده، بسیار دشوار است تا بفهمیم کدام رنگها آن را به وجود آوردهاند. این یکی از اصول مهم رمزنگاری مدرن است: روش رمزنگاری باید در یکجهت بسیار ساده ولی در جهت معکوس بسیار دشوار باشد.
راهحل این است که ابتدا فرد الف و ب بر روی یک رنگ مشترک به شکل عمومی توافق میکنند. فرض کنید این رنگ، زرد باشد. چون این رنگ اعلام عمومی شده، بنابراین فرد ج (شنودکننده) هم به این رنگ دسترسی دارد. سپس فرد الف و ب هرکدام یک رنگ خصوصی را به شکل تصادفی برای خود انتخاب و آن را با رنگ عمومی مخلوط میکنند تا رنگ خصوصی خود را پنهان کنند. سپس فرد الف رنگ خصوصی را پیش خود نگه میدارد و رنگ مخلوط را برای فرد ب میفرستد. به شکل مشابه، فرد ب هم تنها رنگ مخلوط خود را به فرد الف میفرستد. سپس فرد الف و ب هرکدام رنگ خصوصی خود را به رنگ مخلوطی که طرف مقابل فرستاده اضافه میکنند و بهاینترتیب به یک رنگ سرّی مشترک میرسند (شکل-۱۰). علت آنکه هر دو به یک نتیجه رسیدند بسیار ساده است. درواقع هر دو نفر رنگها (زرد، قرمز و سبز) را به روشهای مختلف با یکدیگر ترکیب کردند.
در مقابل، فرد ج گرچه به رنگ مخلوط هر دو فرد دسترسی دارد، چون رنگ خصوصی آنان را نمیداند، نمیتواند به رنگ سرّی مشترک دست پیدا کند (با فرض اینکه جدا کردن رنگ مخلوط شده دشوار است).
دیفی و هلمن الگوریتمی بر مبنای ریاضیات همنهشتی (Modular Arithmetic) پیشنهاد دادند که فرآیند عددی متناظری با فرآیند بالا را انجام دهد. ویژگی اصلی الگوریتم دیفی-هلمن این است که انجام آن در یک جهت ساده ولی در جهت دیگر دشوار است. خوانندگان علاقهمند میتوانند بخش دوم ضمیمه مقاله را برای آشنایی با این الگوریتم مطالعه کنند.
برای آشنایی با الگوریتم RSA که روش دیگری برای رمزنگاری کلید عمومی است، مقاله “رمزنگاری کلید عمومی و امضاء دیجیتال” را مطالعه کنید.
چگونه اعتماد شکل میگیرد؟
ترکیب الگوریتم دیفی و هلمن به همراه استفاده از مولد اعداد شبهتصادفی، کار را برای شنودکننده بسیار دشوار میکند تا بتواند به کلید رمز مشترک دست پیدا کند. ولی ازآنجاکه دو طرف تابهحال هیچ ارتباطی با یکدیگر نداشتند، این امکان وجود دارد که شنودکننده در ارتباط با فرد الف وانمود کند که فرد ب است و کلید عمومی فرد ب را در اختیار دارد. پس فرد الف باید قبل از اجرای این الگوریتم، اطمینان حاصل کند کلید عمومی که از سمت فرد ب میآید واقعاً متعلق به فرد ب است.
یک روش برای ایجاد اطمینان این است که از پروتکلهای مبتنی بر ایجاد اعتماد از طریق شخص سوم (Trusted Third Party) استفاده شود. در این حالت یک شخص سوم که مورد اعتماد همه است اعتبارنامههایی را برای افراد صادر و کلیدهای عمومی آنان را نیز امضاء میکند. بنابراین بهجای اینکه فرد الف بخواهد مستقیماً به فرد ب اعتماد کند، اعتبارنامه او را معیار قرار میدهد. وبسایتهایی که با پروتکل HTTPS (Hypertext Transfer Protocol Secure) کار میکنند، اینگونه هستند.
فرض کنید شما میخواهید برای انجام امور بانکی خود به درگاه یک بانک به نشانی www.bank.ir متصل شوید. وقتی به درگاه بانک وصل میشوید، یک کلید عمومی از طریق نرمافزار مرورگر خود دریافت میکنید. این کلید عمومی برای ساخت یک کلید رمز مشترک با سرور درگاه بانک استفاده میشود تا بعد پیامها از طریق این کلید رمز مشترک به شکل متقارن رمزگذاری شوند. وقتی شما نام کاربری و گذرواژه را در فرم درگاه بانگ وارد میکنید، این اطلاعات بر اساس کلید رمز مشترک رمزگذاری میشوند. تنها سرور بانک که کلید خصوصی متناظر را دارد میتواند این اطلاعات را رمزگشایی کند.
این در حالتی است که شما مطمئن باشید آدرس بالا متعلق به همان بانک است. اگر شنودکننده یک وبسایت جعلی درست کرده باشد، یک کلید عمومی جعلی برای شما ارسال میکند که کلید خصوصی معادل آن را نیز دارد. بهاینترتیب با واردکردن اطلاعات در وبسایت به اطلاعات شما دست پیدا میکند. اینجا جایی است که نقش شخص سوم پررنگ میشود. شخص سوم سازمان معتبری است که کلید عمومی و اطلاعات مالکان همه وبسایتها را دارد. همه نیز این سازمان را میشناسند و کلید عمومی آن سازمان را در اختیار دارند.
وقتی وبسایت بانک از پروتکل HTTPS استفاده میکند، مرورگر کلید عمومی آن وبسایت را که توسط سازمان معتبر امضای دیجیتالی شده دریافت میکند. مرورگر کلید عمومی سازمان معتبر را نیز دارد به همین دلیل میتواند امضای دیجیتال او را تائید کند. درنتیجه مرورگر مطمئن است کلید عمومی به بانک واقعی تعلق دارد. در این حالت سایت جعلی تنها میتواند از کلید عمومی بانک واقعی و نه کلید عمومی دیگری استفاده کند. اما اگر سایت جعلی بخواهد از کلید عمومی واقعی برای رمزنگاری استفاده کند، باید کلید خصوصی متناظر با آن را داشته باشد که امکانپذیر نیست.
برای آشنایی با امضای دیجیتال مقاله “رمزنگاری کلید عمومی و امضاء دیجیتال” را مطالعه کنید.
لازم به ذکر است فنآوریهای جدیدتر مانند زنجیره بلوک بهطور کل از رویکرد متفاوتی برای ایجاد اعتماد بین افراد استفاده میکنند بهطوریکه نیاز به نهاد واسطه را کاملاً حذف کردند.
جمعبندی
در این مقاله من سعی کردم به زبان ساده اصول و مفاهیم رمزنگاری را توضیح دهم. هر یک از این مثالها به جنبههایی از رمزنگاری اشاره میکردند. فکر میکنم در انتها مناسب باشد که همه موارد را مرور کنیم:
مفهوم محرمانگی ایدئال این است که اگر یک پیام ردیابی شود احتمال شکستن رمز پیام پس از ردیابی با احتمال شکستن آن قبل از ردیابی هیچ تفاوتی نکند.
در رمزنگاری مدرن برخلاف گذشته، محرمانگی با پنهانکاری الگوریتمها به دست نمیآید. به همین دلیل است که امروزه نحوه کارکرد الگوریتمهای رمزنگاری کاملاً در دسترس همه قرار دارد. این مسئله کمک کرده است تا خطاهای احتمالی در الگوریتمها شناسایی و برطرف شود.
رمزنگاری مدرن بهطور کامل مبتنی بر الگوریتمهای ریاضی است. مهمترین جنبه این الگوریتمها این است که بر مسائلی در ریاضیات بنا نهاده شدهاند که تاکنون حل آنان با روش سعی و خطا بسیار دشوار بوده است. منظور از بسیار دشوار این است که حل آنان در یکزمان قابلقبول امکانپذیر نیست.
درنهایت اینکه تولید اعداد تصادفی در قلب الگوریتمهای رمزنگاری قرار دارد. البته در این مقاله بحث شد که در عمل ماشینها میتوانند اعداد شبهتصادفی تولید کنند.
***ضمیمه
بخش اول: محاسبه فراوانی حروف در متون فارسی
برای به دست آوردن نمودار فراوانی حروف فارسی، من ابتدا متنهایی را در حوزههای مختلف (سیاسی، تاریخی، علمی، روانشناسی، اقتصادی، ورزشی، ادبی و …) بهصورت تصادفی از وب فارسی جمعآوری کردم. در فایل زیر میتوانید به تجمیع این متنها دسترسی پیدا کنید. درمجموع این متنها شامل بیش از ۱۷ هزار لغت است.
سپس با استفاده از کد زیر در R فراوانی حروف الفبای فارسی را محاسبه کردم.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | # Input letters allLetters <- "آابپتثجچحخدذرزژسشصضطظعغفقکگلمنوهیئؤأء" n = nchar(allLetters) L <- unlist((strsplit(allLetters,"")), use.names = FALSE ) # Input data singleString <- paste(readLines("Text.txt", encoding = "UTF-8")) # Calculate letters' frequency WordCount <- data.frame (L, Count = integer(n)) for (i in 1:n) { WordCount[i,2] <- sum(unlist(strsplit(singleString,"")) == WordCount[i,1]) } WordCount$Frequency = WordCount[,2]/sum(WordCount[,2]) |
بخش دوم: الگوریتم دیفی-هلمن
احتمالاً از ریاضیات دوره دبیرستان به خاطر دارید که اگر یک عدد طبیعی و
و
دو عدد صحیح باشند، میگوییم
در پیمانه
با
همنهشت است اگر و تنها اگر
این جمله را به شکل ریاضی بهاینترتیب نمایش میدهیم:
برای نمونه ۳۰ در پیمانه ۷ با ۹ همنهشت است، چراکه تفاضل ۹ از ۳۰ (که برابر ۲۱ است) بر ۷ بخشپذیر است. توجه کنید ۳۰ در پیمانه ۷ با ۲ نیز همنهشت است.
قبل از ادامه باید یک مطلب دیگر را از ریاضیات همنهشتی مرور کنیم. در ریاضیات همنهشتی عدد را ریشه اولیه به پیمانه
میگوییم هرگاه به ازای هر عددی مانند
که نسبت به
اول است (یعنی مقسومعلیه مشترکشان ۱ است) بتوان عدد صحیحی مانند
یافت که
برای نمونه ۳ ریشه اولیه به پیمانه ۷ است، چراکه
ویژگی مهم در نکته بالا این است که وقتی ریشه اولیه به پیمانه
باشد، اگر
را به توان
برسانیم و حاصل را در پیمانه
محاسبه کنیم، پاسخ با احتمال یکسانی یکی از اعداد بین ۱ تا
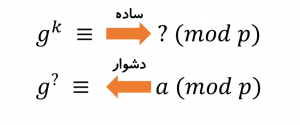
است. به همین دلیل مسیر برگشت دشوار است؛ اگر پاسخ همنهشتی را بدانیم، توانی که
به آن رسیده را نمیتوان بهراحتی یافت و باید با روش سعی و خطا توان را پیدا کرد (شکل-۱۱). اما چقدر دشوار است؟ برای اعداد کوچک زیاد دشوار نیست ولی اگر عدد صدها رقم داشته باشد آنوقت حل مسیر برگشت تقریباً ناممکن میشود. توجه کنید ناممکن به این معنی است که با توان محاسباتی کامپیوترهای امروزی هزاران سال طول میکشد تا مسیر برگشت را حل کرد.
الگوریتم دیفی-هلمن به شکل زیر اجرا میشود:
اول: فرد الف و ب روی مقدار و
تفاهم میکنند (
ریشه اولیه به پیمانه
است). این همان کلید عمومی است. برای نمونه فرض کنید:
دوم: فرد الف یک عدد تصادفی سرّی مانند انتخاب میکند. این همان کلید خصوصی است. فرض کنید مقدار کلید خصوصی فرد الف ۱۵ باشد. سپس مقدار زیر را محاسبه میکند و آن را به شکل عمومی برای فرد ب میفرستد:
سوم: فرد ب نیز یک عدد تصادفی سرّی مانند انتخاب میکند. این هم کلید خصوصی فرد ب است. فرض کنید مقدار کلید خصوصی او ۱۳ باشد. او نیز مقدار زیر را محاسبه میکند و آن را به شکل عمومی برای فرد الف میفرستد:
چهارم: حال فرد الف نتیجه عمومی فرد ب را گرفته و آن را به توان کلید خصوصی خود میرساند و حاصل را در پیمانه محاسبه میکند تا به کلید سرّی مشترک برسد:
پنجم: به شکل مشابه فرد ب نتیجه عمومی فرد الف را گرفته و آن را به توان کلید خصوصی خود میرساند و حاصل را در پیمانه محاسبه میکند تا به کلید سرّی مشترک برسد:
علت آنکه هر دو به یک نتیجه رسیدند بسیار ساده است. درواقع هر دو یک محاسبه را با توالی مختلف انجام دادند:
محاسبه فرد الف:
محاسبه فرد ب:
توجه کنید که همان کلید سرّی مشترک است.
منابع:
Bosworth E. (1992), “Codes”, Encyclopedia Iranica, Vol. V, Fasc. 8, pp. 883-885
Diffie, W., & Hellman, M. (1976). “New Directions in Cryptography”, IEEE Transactions on Information Theory, 22(6), 644-654
Ferguson, N., Schneier, B., & Kohno, T. (2011). “Cryptography Engineering: Design Principles and Practical Applications”, John Wiley & Sons
SURF (2010). “Applications of Modern Cryptography: Technologies, Applications and Choices”, https://www.surf.nl/binaries/content/assets/surf/en/knowledgebase/2010/rapport_201009_SNcryptoWEB.pdf

با سلام
مثال رنگها بسیار جالب بود
چگونه می توان نحوه رمزگذاری در بلاک چین رو با همین مثال توضیح داد
با سلام و تشکر از بیان نظرتان. در خصوص موضوع مورد پرسش مقاله زیر مفید است:
https://analica.ir/cryptography-2/
با سلام و وقت بخیر
مطالب عالی بودن
ممکنه در ارتباط با این نوشته ها اگر مقاله ای دارید برای من ارسال کنید
پروژه کارشناسی بنده در این زمینه است و تنها یک هفته فرصت دارم.ممنون میشم کمک کنید.البته موضوع پروژه بنده رمزنگاری بصری برای تصاویر رنگی است.