قانون لیتل و کاربردهای آن

در مدیریت اصول و قوانین بسیار کمی وجود دارند که بتوان آن‌ها را در شرایط متنوعی بکار برد. قانون لیتل (Little’s Law) در مورد سیستم‌های صف (Queueing Systems) یکی از این موارد استثناء است. این قانون به دلیل سادگی و پیش‌فرض‌های اندکی که بر آن حاکم است، کاربردهای گسترده‌ای دارد. به همین دلیل موردتوجه مدیران است و اغلب می‌توانند با چند محاسبه ساده در حاشیه یک کاغذ به تحلیل‌های خوبی برسند که به آنان در تصمیم‌گیری کمک کند. در این مقاله به قانون لیتل و کاربردهای آن در دنیای واقعی خواهم پرداخت.

ما در زندگی روزمره به‌طور مرتب با سیستم‌های صف مواجه هستیم. صف‌های انتظار را می‌توان در جاهای مختلف مشاهده کرد؛ صندوق فروشگاه‌، ایستگاه مترو یا اتوبوس، ورودی سالن تئاتر یا سینما، اورژانس بیمارستان، تعمیرگاه ماشین‌آلات فرسوده، خط تولید، انبار کارخانه و موارد دیگر. شکل-۱ نمودار یک سیستم صف را نشان می‌دهد. به هر سیستم اقلامی مجزا وارد و از آن خارج می‌شوند. این اقلام می‌توانند انسان‌ها، خودروها، ماشین‌آلات، قطعات در حال ساخت، فعالیت‌های در حال انجام و یا دستورالعمل‌های منتظر برای اجرا در یک سامانه کامپیوتری باشند. اقلام ورودی وارد سیستم می‌شوند، به یک یا تعدادی صف می‌پیوندند و درنهایت، پس از دریافت خدمت از سیستم خارج می‌شوند. در بسیاری موارد این خدمت گلوگاهی است که صف انتظار (Waiting Line) ایجاد می‌کند.

مدت‌زمانی را که اقلام باید در صف بگذراند، مدت‌زمان انتظار (Waiting Time) می‌گویند. در بیشتر موارد زمانی نیز صرف ارائه خدمت (Service Time) در سیستم می‌شود. درصورتی‌که زمان ارائه خدمت طولانی باشد، می‌توان کل زمانی را که فرد در سیستم صف (Time in System) می‌ماند (حاصل جمع زمان انتظار و زمان ارائه خدمت) موردتوجه قرار داد.

قانون لیتل

در سیستم‌های صف متوسط زمان انتظار ( $W$ ) و متوسط تعداد اقلام منتظر برای دریافت خدمت ( $L$ ) دو شاخص مهم هستند. قانون لیتل این دو شاخص را از طریق متوسط نرخ ورود اقلام به سیستم صف ( $\lambda$ ) مرتبط می‌سازد. بر اساس قانون لیتل، تحت شرایط پایدار (Steady State) متوسط تعداد اقلام منتظر برای دریافت خدمت برابر با حاصل‌ضرب متوسط نرخ ورود اقلام به صف در متوسط زمان انتظار در صف است:

$L=\lambda\times W$

در دنیای واقعی، معمولاً دو مورد از سه متغیر بالا را می‌توانیم اندازه‌گیری کنیم و علاقه‌مند به تخمین متغیر سوم هستیم.

قانون لیتل به‌صورت شهودی کاملاً قابل‌فهم است. شکل-۲ با استفاده از استعاره منبع آب این رابطه را نشان می‌دهد. در شرایط پایدار (میزان دبی ورودی و خروجی آب برابر باشد) متوسط حجم آب در مخزن ( $L$ ) برابر حاصل‌ضرب دبی ورودی آب ( $\lambda$ ) در متوسط مدت‌زمانی که یک لیتر آب (یا یک مولکول آن) در منبع باقی می‌ماند ( $W$ ) است. در چنین مثالی $L$ و $\lambda$ را به‌راحتی می‌توان اندازه‌گیری کرد و بر اساس آن $W$ را تخمین زد.

این قانون اولین بار در سال ۱۹۶۱ توسط جان لیتل (John Little) به‌صورت ریاضی ثابت شد و پس‌ازآن جنبه تئوری و کاربردی آن بسیار موردتوجه قرار گرفت. قبل از آن‌که به جنبه‌های کاربردی آن بپردازم، لازم است فرضیات قانون لیتل را مرور کنیم.

فرضیات قانون لیتل در مورد سیستم‌های صف

قانون لیتل دارای دو فرض بسیار مهم است. فرض اول این‌که سیستم باید پایدار باشد. مفهوم این فرض این است که در طول زمان مشاهده سه متغیر اصلی تغییر بنیادی نکنند. برای مثال فرض کنید در صف صندوق فروشگاه، شما متوسط زمان انتظار مشتریان ( $W$ ) را با استفاده از متوسط طول صف ( $L$ ) و سرعت خدمت‌دهی صندوق‌دار ( $\lambda$ ) تخمین زدید. اگر دراین‌بین یک صندوق دیگر برای خدمت‌دهی باز شود، محاسبات دیگر معتبر نیست چراکه در این فاصله سرعت خدمت‌دهی دو برابر شده است. یا اگر در همین مثال دائماً طول صف افزایش پیدا کند، قانون لیتل را نمی‌توان بکار برد، چراکه طول صف ثابت نمانده است. بنابراین لازم است نرخ ورود و خروج مشتریان تقریباً برابر باشد. نکته دیگر این‌که اقلام ورودی باید وارد سیستم شده، در صف بایستند و خدمت را به‌طور کامل دریافت کنند و خارج شوند. برای مثال گفته‌شده، اگر تعداد قابل‌توجهی از مشتریان وقتی به صندوق می‌رسند فعالیت خود را نیمه‌کاره رها کنند و از سیستم خارج ‌شوند، آنگاه فرض پایداری سیستم نقض می‌شود.

فرض دوم این است که واحد استفاده‌شده برای متغیرها باید با یکدیگر سازگار باشد. اگر در مثال بالا متوسط زمان انتظار مشتری برحسب دقیقه سنجیده می‌شود، مقادیر متوسط طول صف و سرعت خدمت‌دهی باید در همان بازه زمانی ارزیابی شوند.

در عمل فرضیات بالا معقول هستند. در بسیاری موارد هنگام مطالعه سیستم یا در بازه‌های زمانی کوتاه، تغییرات اساسی در آن به وجود نمی‌آید.

در اثبات اولیه قانون لیتل فرض شده بود که سیستم به شکل نامتناهی کار می‌کند مانند یک خط تولید ۲۴ ساعته که در بازه زمانی نامتناهی به شکل پیوسته در حال فعالیت است. این رابطه بعدها به حالات دیگری از صف نیز تعمیم داده شد که به صف‌های دنیای واقعی نزدیکی بیشتری دارند.

بسیار پیش می‌آید که یک سیستم در یک ‌زمان شروع به فعالیت می‌کند و در زمان دیگری فعالیتش را خاتمه می‌دهد. معمولاً نیز سیستم در ابتدا و انتهای فعالیت خود بیکار است (شکل-۳). در مثال فروشگاه در زمان شروع و پایان فعالیت صندوق، عملاً مشتری وجود ندارد. بنابراین متغیرها ثابت نمی‌مانند و فرض پایداری سیستم نقض می‌شود. خوشبختانه ثابت شده که قانون لیتل را در این موارد نیز می‌توان بکار برد.

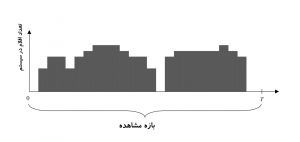
اگر در ابتدا و انتهای بازه زمانی محدود، تعداد اقلام صفر نباشد بازهم می‌توان قانون لیتل را بکار برد (شکل-۴). به‌عنوان نمونه در انبارها تعداد اقلام موجود بیشتر مواقع در یک سطح معین که به آن ذخیره اطمینان (Safety Stock) می‌گوییم حفظ می‌شود تا از نبود جنس موردنظر مشتری در زمان مراجعه جلوگیری شود.

قانون لیتل چه فرضیاتی ندارد

فرضیات محدود قانون لیتل، اعتبار و قابلیت به‌کارگیری آن را بالا برده است. زیبایی قانون لیتل در این است که نیاز به بسیاری از فرضیات در مورد سیستم صف ندارد. این‌که توزیع متغیر نرخ ورود یا خروج چه باشد (برای مثال توزیع نرمال) اهمیتی ندارد. این‌که ترتیب خدمت‌دهی در سیستم چگونه باشد (برای مثال خدمت‌دهی بر اساس ورود FIFO) اهمیتی ندارد. این‌که شما رابطه را برای کل سیستم بکار می‌برید یا قسمتی از آن مهم نیست (برای مثال برای یک صندوق‌دار فروشگاه بکار می‌برید یا کل صندوق‌داران فروشگاه). این‌که سیستم دارای یک یا چند خدمت دهنده یا صف باشد نیز اهمیتی ندارد. تنها لازم است دو فرض اشاره‌شده معتبر باشد.

مثال‌هایی از کاربرد قانون لیتل

خرده‌فروشی

فرض کنید در یک خرده‌فروشی، مشاهدات میدانی نشان می‌دهد به‌طور متوسط ۵ نفر در صف صندوق می‌ایستند. اگر صندوق‌دار در هر دقیقه به ۲ مشتری خدمت دهد، می‌توان گفت به‌طور متوسط زمان انتظار هر مشتری ۲٫۵ دقیقه است:

$W = L / \lambda = 5(customers)/2(customers/minutes) = 2.5 (minutes)$

محاسبات را می‌توان به کل فروشگاه نیز تعمیم داد. اگر مشاهدات میدانی نشان دهد در هرلحظه به‌طور متوسط ۳۰ نفر در فروشگاه مشغول خرید هستند، می‌توان گفت به‌طور متوسط هر مشتری ۱۵ دقیقه از زمان خود را در فروشگاه سپری می‌کند:

$W = L / \lambda = 30(customers)/2(customers/minutes) =15 (minutes)$

شما به‌عنوان مدیر فروشگاه می‌توانید اعداد بالا را با اهداف تعیین‌شده یا رقبای خود مقایسه کنید. شاید با مقایسه این اعداد به نتیجه برسید زمان انتظار در صف نسبتاً مناسب است ولی بهتر بود اگر مشتریان زمان بیشتری را در فروشگاه سپری کنند چراکه هرچه بیشتر در فروشگاه بمانند، احتمال خرید کردنشان هم بیشتر می‌شود!

بیمارستان

شما به‌عنوان مشاور یک بیمارستان محلی، می‌خواهید برآوردی از تعداد تخت‌ها و نیروی انسانی موردنیاز بخش زایمان داشته باشید. داده‌های تاریخی نشان داده در آن منطقه به‌طور متوسط ۵ زایمان در روز رخ می‌دهد. در ۹۰ درصد مواقع مادران نیاز دارند ۲ روز در بیمارستان بستری شوند. در ۱۰ درصد دیگر موارد لازم است تا مادران ۷ روز در بیمارستان بمانند. بنابراین می‌توان گفت به‌طور متوسط مادران ۲٫۵ روز در بیمارستان بستری هستند:

$W=0.9 \times2+0.1\times7=2.5 (days)$

با داشتن اطلاعات بالا و به‌کارگیری قانون لیتل، می‌توان گفت در هرروز در این بیمارستان حدود ۱۳ نفر بستری هستند:

$L= W\times\lambda=2.5(days)\times5(mothers/day) =12.5 (mothers)$

این برآورد به شما کمک می‌کند تعداد تخت خواب موردنیاز و نیروی انسانی بخش زایمان را تخمین بزنید. البته باید توجه کرد که آنچه قانون لیتل به دست می‌دهد میانگین است. سیستم‌ها دارای واریانس هستند. در یک بیمارستان شاید هدف این باشد تا در بیشتر موارد هیچ مراجعه‌کننده‌ای بی‌پاسخ گذاشته نشود. در این حالت نیاز بیمارستان به تخت خواب بیش از ۱۳ است. روشی مانند شبیه‌سازی مونت‌کارلو (Monte Carlo Simulation) کمک می‌کند تا راه‌حل میانی برای ایجاد تعادل بین بی‌پاسخ گذاشتن مراجعان و وجود ظرفیت اضافه در سیستم پیدا کنیم. ولی آنچه قانون لیتل به دست می‌دهد شروع خوبی برای برآورد ابتدایی است.

سرمایه‌گذاری

یکی از دوستان شما که صاحب یک بوفه صبحانه است از شما دعوت کرده که در کسب‌وکار او سرمایه‌گذاری کنید. دانستن تخمینی از میزان درآمد او به شما کمک می‌کند تا با اطلاعات بهتری در مورد این سرمایه‌گذاری تصمیم بگیرید. به این منظور در چند ماه گذشته به‌صورت تصادفی در بازه زمانی ۶ تا ۹ صبح به بوفه او سرزده‌اید. مشاهدات شما نشان می‌دهد به‌طور متوسط ۱۰ مشتری در بوفه او در صف انتظار هستند و تقریباً ۵ دقیقه طول می‌کشد تا هر مشتری وارد و از بوفه خارج شود. اگر فرض کنیم این مشاهدات نمونه خوبی از وضعیت سیستم است، با استفاده از قانون لیتل می‌توان گفت این بوفه به‌طور متوسط در هر ساعت ۱۲۰ مشتری دارد:

$\lambda=L/W=10(customers)/5(minutes)= 2 (customers/minute)=120(customers/hour)$

با توجه به منوی بوفه می‌توانید برآورد کنید هر مشتری به‌طور متوسط چقدر در بوفه خرج می‌کند و درآمد ساعتی و سپس ماهیانه بوفه را حساب کنید.

استارتاپ

شما مدیر یک پیام‌رسان داخلی هستید که در رقابت با سایر پلتفرم‌های موجود به دنبال جذب کاربر هستید. پس از یک سال تلاش، موفق به جذب ۵ میلیون کاربر شده‌اید. داده‌های پلتفرم نشان می‌دهد حدود ۲ میلیون ۴۰۰ هزار کاربر در هرروز به پیام‌رسان شما مراجعه می‌کنند و به‌طور متوسط ۲۰۰ هزار کاربر هم‌زمان در سیستم شما وجود دارند.

در چنین پلتفرم‌هایی نباید تنها به تعداد کاربر توجه داشت. مدت‌زمانی که کاربران در پلتفرم شما باقی می‌مانند هم به جهت زیرساخت‌های فنی و هم به جهت بازاریابی اهمیت دارد. برای این مثال قانون لیتل نشان می‌دهد که کاربران به‌طور متوسط ۲ ساعت در پلتفرم شما سپری می‌کنند:

$W = L / \lambda = 200k(users)/2400k(users/day) =0.0833 (day)\approx 2(hours)$

فرض کنید یک نظرسنجی در مورد رفتار کاربران ایرانی در پیام‌رسان‌ها نشان داده که آنان ۵ ساعت در روز را در پیام‌رسان رقیب سپری می‌کنند. به‌این‌ترتیب اگرچه به لحاظ تعداد کاربران رشد خوبی تجربه ‌شده، برای باقی ماندن در فضای رقابتی لازم است سیاست‌هایی اتخاذ کنید تا کاربران را تشویق کند وقت بیشتری در پیام‌رسان بگذرانند.

تعمیرگاه

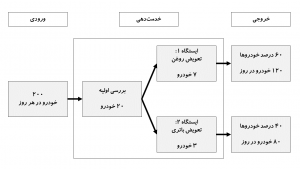
فرض کنید که در یک تعمیرگاه خودرو دو نوع خدمت استاندارد عرضه می‌شود. فرآیند به این صورت است که خودروها در بدو ورود برای دریافت خدمت ثبت‌نام می‌کنند و یک بررسی عمومی می‌شوند. در ایستگاه کاری ۱ تعویض باتری صورت می‌گیرد و در ایستگاه کاری ۲ روغن‌موتور تعویض می‌شود. همان‌طور که در شکل-۵ دیده می‌شود، به‌صورت روزانه ۲۰۰ خودرو به این تعمیرگاه مراجعه می‌کنند.

همه خودروها از مرحله ثبت‌نام و بررسی عبور می‌کنند. به‌طور متوسط در این مرحله ۲۰ خودرو وجود دارند.
حدود ۶۰ درصد مشتریان درخواست تعویض روغن دارند. متوسط خودروها در این مرحله ۷ خودرو است.
۴۰ درصد دیگر خودروها نیاز به تعویض باتری دارند. متوسط خودروها در این مرحله ۳ خودرو است.

با در نظر گرفتن این سناریو می‌توانیم تحلیل‌های زیر را انجام دهیم:

زمان انتظار (W) برای بررسی عمومی برابر است با:

$W = L / \lambda = 20(cars)/200(cars/day) =0.1 (day)= 48(minutes)$

متوسط زمان انتظار خودروها در ایستگاه ۱ برابر است با:

$W = L / \lambda = 7(cars)/0.6\times200(cars/day) =0.0583 (day)= 28(minutes)$

به همین ترتیب، متوسط زمان انتظار در بخش تعویض باتری برابر است با:

$W = L / \lambda = 3(cars)/0.4\times200(cars/day) =0.0375 (day)= 18(minutes)$

محاسبات بالا نشان می‌دهد که اگر مشتری بخواهد تعویض روغن انجام دهد به‌طور متوسط ۷۶ دقیقه در تعمیرگاه است. اگر مشتری بخواهد تعویض باتری کند، باید در کل ۶۶ دقیقه منتظر بماند. همچنین محاسبات بالا نشان می‌دهد هر مشتری بیش از یک ساعت در تعمیرگاه سپری می‌کند. این می‌تواند آزاردهنده باشد. مدیر تعمیرگاه شاید به این فکر کند چگونه فرآیند عملیاتی را بهبود ببخشد تا زمان انتظار مشتری را در سیستم کاهش دهد، شاید هم لازم نباشد مشتری در تمامی این یک ساعت در تعمیرگاه حضور داشته باشد و شاید به این فکر کند چگونه تجربه مشتری را از انتظار در سیستم دل‌پذیرتر کند.

نکته دیگر این‌که همان‌طور که در مثال بالا دیدید، قانون ساده اما کاربردی و قدرتمند لیتل را می‌توان برای یک فرآیند یا تعداد متعددی فرآیند بکار برد.

نکاتی پیرامون به‌کارگیری قانون لیتل

باید توجه داشت که قانون لیتل با مقادیر متوسط متغیرها کار می‌کند. در مقاله “خطا در استفاده از میانگین” توضیح داده ‌شده است که استفاده از میانگین در برآوردها در چه زمان‌هایی و چگونه می‌تواند مدیران را گمراه کند. باید توجه کرد که قانون لیتل تنها یک برآورد اولیه در اختیار مدیران قرار می‌دهد. بسته به اهمیت موضوع برای سیاست‌گذاری به‌منظور بهبود سیستم روش‌های دقیق‌تر مانند استفاده از تئوری صف (Queueing Theory) یا شبیه‌سازی (Simulation) پیشنهاد می‌شود.

نکته مهم دیگر این‌که قانون لیتل را وقتی می‌توان بکار برد که به گذشته سیستم نگاه می‌کنیم (تحلیل پس‌نگر Backward Looking Analysis). خطای رایج در استفاده از قانون لیتل این است که از آن برای پیش‌بینی آینده سیستم استفاده شود. برای مثال نمی‌توان گفت اگر تعداد خدمت‌دهندگان را دو برابر کنیم، مطابق قانون لیتل زمان انتظار نصف می‌شود؛ در این حالت ممکن است زمان انتظار کمتر شود، بیشتر شود و یا تغییری نکند. یکی از رفتارهای خلاف شهود سیستم‌های صف بروز رفتارهای غیرخطی است. توجه کنید قانون لیتل تنها در شرایطی که فرض پایداری سیستم برقرار است، مصداق دارد. وقتی تغییری در یک متغیر ایجاد می‌شود، سیستم از حالت پایدار خارج می‌شود. وقتی سیستم به حالت پایدار جدید رسید، دوباره می‌توان قانون لیتل را برای آن بکار گرفت.

اگر مطالب این مقاله برایتان جالب بود، توصیه می‌کنم مقاله “چرا درک سیستم‌های ذخیره–جریان اهمیت دارد؟” را هم مطالعه کنید.

منابع:

Bendoly, E., van Wezel, W., & Bachrach, D. G. (Eds.). (2015). “The Handbook of Behavioral Operations Management: Social and Psychological Dynamics in Production and Service Settings”, Oxford University Press

Chhajed, D., & Lowe, T. J. (Eds.). (2008). “Building Intuition: Insights from Basic Operations Management Models and Principles (Vol. 115)”, Springer Science & Business Media

Ivanov, D., Tsipoulanidis, A., & Schönberger, J. (2016). “Global Supply Chain and Operations Management: A Decision-Oriented Introduction to the Creation of Value”, Springer

Little, J. D. (2011). “OR FORUM—Little’s Law as Viewed on Its 50th Anniversary”, Operations Research, 59(3), 536-549

3 نظر در “قانون لیتل و کاربردهای آن”

رضا صدرایی
بهمن ۲۸, ۱۳۹۷ در ۱۱:۵۹ ق٫ظ
پیوند یکتا
درود و سپاس از مقاله شیوا و آموزنده شما
در مورد یک رستوران که در فصول مختلف شرایط مختلفی دارد آیا می توان سال را به مقاطع کوتاه تر تقسیم کرد سپس در هر مقطع محاسبات را انجام داد و سپس از نتایج مقاطع براوردی برای سال یک رستوران بدست آورد؟ و این براورد چگونه انجام می شود؟
پاسخ
- فرزاد مینویی
  اسفند ۴, ۱۳۹۷ در ۶:۳۷ ب٫ظ
  پیوند یکتا
  با سلام،
  توجه کنید که قانون لیتل فرضی برای الگوی توزیع متغیر نرخ ورودی ندارد، تنها فرض درباره پایداری سیستم است. شما باید بازه زمانی را انتخاب کنید که مطمئن شوید هرچه وارد سیستم شده تقریبا با همان نرخ از آن خارج شده است.
  بنابراین در حالتی که تقاضای رستوران از الگوی فصلی هم پیروی می کند می توان قانون لیتل را بکار برد. تنها باید توجه کرد قانون لیتل با مقادیر متوسط کار می کند. در شرایط وجود تقاضای فصلی واریانس بالاتر از زمانی است که الگوی تقاضا نسبتا ثابت است و خطای برآورد از قانون لیتل بالاتر می رود. پس یک راه این است که قانون لیتل را برای بازه های زمانی که الگوی تقاضا یکسان است، بکار برد.
  پاسخ
مهسا خراسانی
بهمن ۱, ۱۳۹۸ در ۴:۲۲ ب٫ظ
پیوند یکتا
سلام، بسیار عالی و قابل فهم عنوان شده بود .???
پاسخ

آنالیکا