در این مقاله توضیح میدهم که اگر بخواهیم دادههای موجود در جامعه آماری و یا نمونه را تنها با یک عدد نشان دهیم از چه شاخصهایی میتوانیم استفاده کنیم. هدف استفاده از چنین شاخصهایی این است که اطلاعاتی را که در مجموعه دادهها وجود دارد در یک مقدار عددی خلاصه کند. شاخصهایی مانند میانگین (Mean)، میانه (Median) و مد (Mode) برای چنین منظوری بکار میروند. این شاخصها در آمار تحت عنوان سنجههای گرایش به مرکز (Measures of Central Tendency) شناخته میشوند.
میانگین حسابی
مجموع مقادیر محاسبهشده تقسیمبر تعداد مشاهدات میانگین حسابی (Arithmetic Mean) را به دست میدهد. میانگین حسابی که عمدتاً در زبان فارسی بهاختصار میانگین نامیده میشود، یکی از رایجترین شاخصهایی است که در مدیریت و کسبوکار برای خلاصهسازی دادهها استفاده میگردد. معمولاً در آمار میانگین جامعه آماری با و میانگین نمونه با (bar)x نشان داده میشوند.
میانگین جامعه آماری زمانی بکار میرود که دادهها نماینده تمام عناصر موجود در جمعیت موردمطالعه باشند و از رابطه زیر محاسبه میشود:
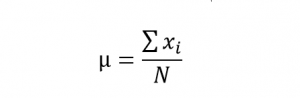 در رابطه بالا
در رابطه بالا نشاندهنده مقدار
ام و
تعداد مقادیر دادهها در جمعیت است.
میانگین نمونه همزمانی بکار میرود که دادهها نشاندهنده نمونهای از جمعیت موردمطالعه باشند و از رابطه زیر محاسبه میشود:
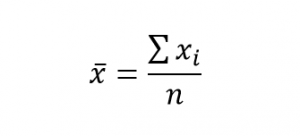 در رابطه بالا
در رابطه بالا نشاندهنده مقدار
ام و
تعداد مقادیر دادهها در نمونه آماری است.
در عمل دو رابطه بالا یکی هستند ولی نحوه نمایش آن در آمار برای میانگین جامعه و نمونه متفاوت است.
در نرمافزار اکسل (Excel) از تابع ()AVERAGE برای محاسبه میانگین استفاده میشود. فرض کنید میزان تقاضای ماهیانه یک شرکت در ۱۲ ماه گذشته مطابق شکل-۱ است. خانه C15 میانگین دادهها را با استفاده از فرمول زیر به دست میدهد:
AVERAGE(C3:C14)=
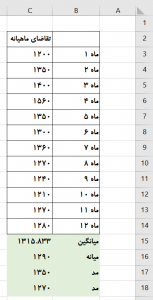
در زبان R برای محاسبه میانگین دادهها از تابع ()mean استفاده میشود. در کد زیر ابتدا دادههای تقاضا وارد نرمافزار و به شکل دیتا فریم (Data Frame) ذخیره شدهاند. سپس میانگین دادهها محاسبه شده است.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | #Input data Input = (" Month Demand M1 1200 M2 1350 M3 1400 M4 1560 M5 1350 M6 1300 M7 1360 M8 1270 M9 1240 M10 1210 M11 1270 M12 1280 ") Data = read.table(textConnection(Input), header = TRUE) #Arithmetic Mean mean(Data$Demand) [1] 1315.833 |
توجه کنید چون در محاسبه میانگین از تمام دادههای موجود استفاده میشود، میانگین تحت تأثیر مقادیر انتهایی (Extreme Values) قرار میگیرد. فرض کنید در مثال گفتهشده مقدار بیشینه تقاضا که مربوط به ماه چهارم است، از ۱۵۶۰ به ۳۰۰۰ تغییر کند. در این صورت همین تغییر موجب افزایش ۹ درصدی میانگین میشود.
اگر میخواهید بدانید در چه زمانی نباید از میانگین استفاده کرد، مقاله “خطا در استفاده از میانگین” را مرور کنید.
میانگین وزنی
زمانی که برخی از مقادیر در دادهها مهمتر از برخی دیگر باشند، میانگین وزنی استفاده میشود. در این حالت وزن هر مقدار () نشاندهنده اهمیت نسبی آن است. رابطه ریاضی محاسبه میانگین وزنی برای جمعیت (
) یا نمونه (
) به ترتیب زیر است:
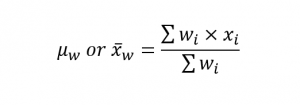 میانه
میانه
اگر دادهها به ترتیب از کوچکتر به بزرگتر مرتب شوند، نیمی از آنها از میانه کوچکتر و نیمی دیگر از میانه بزرگتر هست. اگر تعداد اعداد فرد باشد، عدد وسطی میانه است. اگر تعداد زوج باشد میانه برابر میانگین دو عدد وسطی خواهد بود. در مثال بالا اگر اعداد را مرتب کنیم به سری زیر میرسیم:
۱۲۰۰,۱۲۱۰,۱۲۴۰,۱۲۷۰,۱۲۷۰,۱۲۸۰,۱۳۰۰,۱۳۵۰,۱۳۵۰,۱۳۶۰,۱۴۰۰,۱۵۶۰
چون تعداد زوج است، میانه برابر میانگین ۱۳۰۰ و ۱۲۸۰ یعنی ۱۲۹۰ است.
در نرمافزار اکسل از تابع ()MEDIAN برای محاسبه میانه استفاده میشود. برای مثالی که در شکل-۱ آمده است، میانه اعداد با استفاده از فرمول این به دست میآید:
MEDIAN(C3:C14)=
در زبان R برای محاسبه میانگین دادهها از تابع ()median استفاده میشود.
1 2 3 | #Median median(Data$Demand) [1] 1290 |
لازم به ذکر است میانه تحت تأثیر مقادیر انتهایی نیست. اگر مقدار بیشینه تقاضا به ۳۰۰۰ تغییر کند، هیچ تغییری در میانه دادهها رخ نمیدهد.
مد
در یک مجموعه از دادهها، مد مقداری است که بیش از همه تکرار شده است. مانند میانه، مد نیز تحت تأثیر مقادیر انتهایی قرار نمیگیرد. در مثال گفتهشده دادهها دارای دو مد هستند. مقادیر ۱۳۵۰ و ۱۲۷۰ هرکدام دو بار تکرار شدهاند و دارای بیشترین فرکانس وقوع هستند.
در نرمافزار اکسل از تابع ()MODE.SNGL و یا ()MODE. MULT برای محاسبه مد استفاده میشود (شکل-۱).
در زبان R تابع مشخصی برای محاسبه مد تعریف نشده است. برای این منظور من تابعی را با نام GetMode در R تعریف کردم. در این تابع ابتدا با استفاده از ()unique مقادیر یکتا در دادههای ورودی (x) به دست میآیند و در متغیر u قرار میگیرند. سپس تابع ()match تعیین میکند هر مقدار در بردار u در چه جایگاهی در بردار ورودی (x) قرار دارد. تابع ()tabulate مشخص میکند مقادیر عدد صحیح چند بار تکرار شدهاند. ساختار which(vector == max(vector)) مقادیر بیشینه را در یک بردار عددی مشخص میکند. درنهایت این دستور داده میشود تا عناصر متناظر با این مقادیر بیشینه در بردار u فراخوانی شوند.
1 2 3 4 5 6 7 8 9 10 | #Mode #Creat the function GetMode= function(x) { u = unique (x) u[which((tabulate(match(x, u))) == max((tabulate(match(x, u)))))] } #Calculate the mode using the function GetMode(Data$Demand) [1] 1350 1270 |
برای راحتی تنها لازم است بخش تابع را در R کپی کنید و با فراخوانی تابع تعریفشده مقدار مد را برای دادههای خود محاسبه کنید.
جهت یادآوری باید اشاره کرد که میانگین از تمامی دادهها موجود استفاده میکند و تصویر کاملتری از داده به دست میدهد. ولی میتواند به شدن تحت تأثیر مقادیر کمینه یا بیشینه قرار گیرد. همچنین برای یک مجموعه از اعداد یک میانگین و میانه قابلتعریف است. درحالیکه ممکن است یک مجموعه اعداد دارای یک یا چند مد باشد.
میانگین هندسی
برخی موارد بهجای میانگین حسابی باید از میانگین هندسی (Geometric Mean) استفاده کرد. معمولاً در حوزه اقتصاد و مدیریت میانگین هندسی برای بیان نرخ تغییر یک متغیر در طول زمان بکار میرود. برای محاسبه میانگین متغیرهایی مانند تورم، نرخ بهره مرکب، رشد اقتصادی و مانند آن از این نوع میانگین استفاده میشود.
میانگین هندسی مقدار از رابطه زیر محاسبه میگردد:
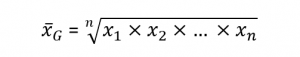 برای نمونه اگر بخواهیم از رابطه بالا برای محاسبه نرخ میانگین بازگشت سرمایه (
برای نمونه اگر بخواهیم از رابطه بالا برای محاسبه نرخ میانگین بازگشت سرمایه () در یک دوره زمانی شامل
بازه استفاده کنیم، محاسبات به ترتیب زیر خواهد شد:
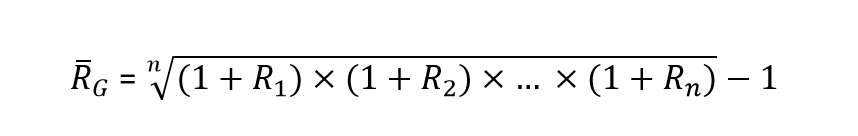 در رابطه بالا
در رابطه بالا نرخ بازگشت روی سرمایه در دروه زمانی
ام است.
برای روشن شدن علت استفاده از میانگین هندسی در این شرایط به این مثال توجه کنید. فرض کنید شما در ابتدای سال ۱۰۰ هزار دلار سرمایهگذاری کردید و در انتهای سال ۵۰ هزار دلار را از دست میدهید. سپس در انتهای سال دوم دوباره سرمایه شما به ۱۰۰ هزار دلار برمیگردد. برای این سرمایهگذاری نرخ بازده در سال اول ۵۰- درصد و در سال دوم ۱۰۰ درصد است. اگر از میانگین حسابی استفاده کنید نرخ میانگین برای این دو سال ۲۵ درصد به دست میآید. درحالیکه میانگین نرخ بازده برای دو سال از رابطه بالا مبتنی بر میانگین هندسی صفر درصد است. در عمل نیز در طول این دو سال ارزش این سرمایهگذاری تغییری نکرده و میانگین هندسی به شکل دقیقتری منعکسکننده تغییرات ارزش سرمایهگذاری است.
در نرمافزار اکسل از تابع ()GEOMEAN میتوان استفاده کرد. در زبان R تابع از پیش تعریفشدهای وجود ندارد. برای محاسبه میانگین هندسی تابعی را با نام GM.Mean در R به شکل زیر تعریف کردم. توجه کنید در تعریف این تابع فرض شده است که دادهها بزرگتر از صفر هستند.
1 2 3 4 5 6 7 8 9 | #Creat the function GM.Mean = function(x){ exp(mean(log(x))) } #Calculate the geometric mean using the function data = c(0.1, 0.2, 0.25, 0.31, 0.42, 0.37) GM.Mean(data) [1] 0.2494387 |
منابع:
Levine, D. M., Berenson, M. L., & Stephan, D. (1999). “Statistics for Managers Using Microsoft Excel”, Upper Saddle River, NJ: Prentice Hall
Weiers, R. M. (2010). “Introduction to Business Statistics”, Cengage Learning

مطالب قابل درک ، ممنون
سلام. یه سوال:
چرا میانگین نسبت به مقادیر انتهایی (extreme) حساس هست و چگونه میشه این حساسیت رو کم کرد؟؟؟