شاخص‌های پراکندگی در آمار

اگرچه میانگین و سایر شاخص‌های مرکزی کمک می‌کنند تا مرکز داده‌ها را در جامعه یا نمونه آماری تشخیص دهیم، تنها اکتفا کردن به این شاخص‌ها می‌تواند تصویر نادرستی از مسئله پیش روی ما بگذارد. در بسیاری موارد فهمیدن این‌که داده‌ها چگونه حول میانگین پراکنده شده‌اند اهمیت پیدا می‌کند.

اگر می‌خواهید بدانید در چه زمانی نباید از میانگین استفاده کرد، مقاله “خطا در استفاده از میانگین” را مرور کنید.

فرض کنید سه دستگاه خودکار دارید که بسته‌های حاوی پسته را پر می‌کند. شکل-۱ توزیع وزن بسته‌های خروجی از این سه دستگاه را برحسب اونس (Ounce) نشان می‌دهد. هدف این است که هر بسته حاوی حدود ۱۲ اونس پسته باشد.

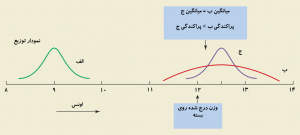
از نمودارهای شکل-۱ مشخص است که دستگاه الف میزان کمتری ازآنچه لازم است پر می‌کند. میانگین وزنی بسته‌های خروجی از این دستگاه ۹ اونس است که با میزان درج‌شده روی بسته تفاوت دارد. با احتمال زیاد بیشتر مشتریان بسته‌هایی با وزن بسیار کمتر از میزان ادعاشده روی بسته دریافت خواهند کرد. این مسئله موجب نارضایتی مشتریان و حتی ایجاد تبعات حقوقی برای آن شرکت می‌شود.

میانگین وزنی بسته‌های خروجی دستگاه ب و ج هر دو ۱۲٫۵ اونس است که کمی بیش از میزان درج‌شده روی بسته است. ولی پراکندگی وزن بسته‌های خروجی از دستگاه ب نسبت به دستگاه ج بیشتر است. به این معنی که بسته‌های بیشتری وجود دارند که ممکن است وزنشان کمتر از میزان ادعاشده روی بسته باشد. با احتمال متوسطی ممکن است برخی مشتریان ناراضی شوند و شکایت حقوقی طرح کنند.

وزن بسته‌های خروجی از دستگاه ج دارای میانگین ۱۲٫۵ اونس هستند و حول این میانگین به شکل فشرده‌تری توزیع شده‌اند. در این حالت احتمال بسیار کمی وجود دارد که مشتریان بسته‌ای دریافت کنند که وزن آن کمتر از وزن درج‌شده باشد.

این مثال نشان می‌دهد چگونه مفهوم پراکندگی در دنیای کسب‌وکار می‌تواند دلالت‌هایی داشته باشد. در مقاله “چرا درک واریانس اهمیت دارد؟” با مثال‌های مختلف از دنیای واقعی به دلالت‌های مفهوم پراکندگی پرداخته‌ام. در این مقاله به شاخص‌های پراکندگی (Measures of Dispersion) در آمار شامل دامنه (Range)، چارک‌ها (Quartiles)، واریانس (Variance) و انحراف معیار (Standard Deviation) می‌پردازم.

دامنه

ساده‌ترین شاخص پراکندگی دامنه است که تفاوت بین بزرگ‌ترین و کوچک‌ترین مقدار است. فرض کنید از بسته‌های خروجی دستگاه ج یک نمونه تصادفی ۲۰ تایی گرفته و وزن کرده‌ایم. شکل-۲ وزن این نمونه‌ها را نشان می‌دهد. برای محاسبه دامنه در نرم‌افزار اکسل (Excel) باید بیشینه و کمینه را به دست آوریم و تفاوت آن‌ها را محاسبه کنیم. در شکل-۲ در خانه E4 دامنه از رابطه زیر محاسبه شده است.

MAX(C3:C22)-MIN(C3:C22)=

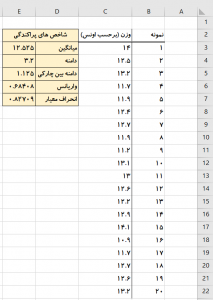
در زبان R هم می‌توان به‌طور مشابه از ترکیب دو تابع ()max و ()min دامنه را محاسبه کرد. در مثال بالا ابتدا داده‌ها وارد و به شکل دیتا فریم (Data Frame) ذخیره شده‌اند. سپس میانگین و دامنه داده‌ها محاسبه شده است.

#Input data

Input = ("Weight.Ounces 14.0 12.5 13.2 11.7 11.9 12.4 12.7 11.9 11.2 13.1 13.0 12.6 12.2 12.9 14.1 10.9 11.7 12.7 12.6 13.2")

Data = read.table(textConnection(Input), header = TRUE)

#Mean

mean(Data$Weight.Ounces)

[1] 12.525

#Range

max(Data$Weight.Ounces) - min(Data$Weight.Ounces)

[1] 3.2

اگرچه محاسبه دامنه ساده است، اطلاعات زیادی در مورد پراکندگی داده‌ها نمی‌دهد و تنها وابسته به مقادیر ابتدایی و انتهایی است. اما آنچه در این بین می‌گذرد مشخص نیست. چارک‌ها می‌توانند در این خصوص اطلاعات بیشتری بدهند.

چارک‌ها

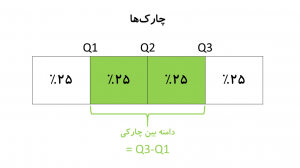
در قبل توضیح داده شد که میانه داده‌ها را به دو قسمت مساوی تقسیم می‌کند؛ مقادیری که از میانه بزرگ‌ترند و آن‌هایی که از میانه کوچک‌ترند. چارک داده‌ها را به چهار قسمت مساوی تقسیم می‌کند؛ هر بخش شامل ۲۵ درصد مشاهدات است. میانه چارک دوم محسوب می‌شود که ۵۰ درصد مشاهدات از آن کوچک‌تر و ۵۰ درصد مشاهدات از آن بزرگ‌تر هستند. با فرض آنکه $N$ مشاهده وجود داشته باشد، اگر داده‌ها را از کوچک‌تر به بزرگ‌تر مرتب کنید مقادیر چارک اول تا سوم از روش زیر محاسبه می‌شود:

چارک اول (Q1) مقداری است که در جایگاه $(N+1)/4$ ام قرار دارد.

چارک دوم (Q2) مقداری است که در جایگاه $2(N+1)/4$ ام قرار دارد.

چارک سوم (Q3) مقداری است که در جایگاه $3(N+1)/4$ ام قرار دارد.

برخلاف دامنه که به مقادیر انتهایی (Extreme Values) وابسته است، چارک‌ها این امکان را می‌دهند که دید بهتری از توزیع داده‌ها داشته باشیم. بر مبنای چارک‌ها شاخص دامنه بین چارکی (Interquartile Range) تعریف می‌شود که تفاوت بین چارک سوم و چارک اول است. این شاخص نشان می‌دهد که فاصله بین ۷۵ و ۲۵ درصد مقادیر چقدر است (شکل-۳).

در نرم‌افزار اکسل از تابع ()QUARTILE برای محاسبه چارک‌ها می‌توان استفاده کرد. به‌این‌ترتیب که در ابتدا محدوده داده‌ها وارد و سپس به‌عنوان پارامتر دوم باید مشخص کرد قرار است کدام‌یک از چارک‌ها محاسبه شوند. برای محاسبه دامنه بین چارکی کافی است تفاوت بین چارک سوم و اول محاسبه گردد. در مثال قبل دامنه بین چارکی در خانه E5 به ترتیب زیر محاسبه شده است:

QUARTILE(C3:C22,3)-QUARTILE(C3:C22,1)=

در زبان R با استفاده از تابع ()quantile تمامی چارک‌ها محاسبه می‌شوند. تابع ()IQR نیز برای محاسبه دامنه بین چارکی استفاده می‌شود. در مثال قبل کد زیر برای محاسبه این شاخص‌ها بکار می‌روند:

#Quartiles and Interquartile range

quantile(Data$Weight.Ounces)

0% 25% 50% 75% 100%

10.900 11.900 12.600 13.025 14.100

IQR(Data$Weight.Ounces)

[1] 1.125

واریانس و انحراف معیار

در دنیای کسب‌وکار واریانس یکی از پرکاربردترین شاخص‌ها برای نشان دادن میزان پراکندگی داده‌ها است. در محاسبه این سنجه برخلاف قبلی‌ها از تمامی داده‌ها استفاده می‌شود. واریانس به زبان ساده میانگین مجذور فاصله داده‌ها از مرکز آن‌هاست. واریانس برای جمعیت آماری با $\sigma^{2}$ نشان داده می‌شود و از رابطه زیر به دست می‌آید:

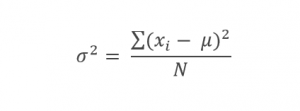
در رابطه بالا $x_{{i}}$ نشان‌دهنده مقدار $i$ ام، $N$ تعداد مقادیر داده‌ها و $\mu$ میانگین جمعیت است.

واریانس برای نمونه آماری با $s ^{2}$ نشان داده می‌شود و از رابطه زیر به دست می‌آید:

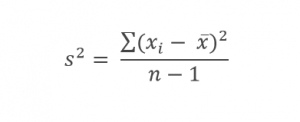در رابطه بالا $x_{{i}}$ نشان‌دهنده مقدار $i$ ام، $n$ تعداد مقادیر داده‌ها در نمونه آماری و $x(bar)$ میانگین آن است. به‌منظور محاسبه واریانس نمونه آماری در مخرج کسر از $n-1$ استفاده می‌شود چراکه این شاخص برای واریانس جامعه آماری که نمونه از آن استخراج شده، برآوردکننده بهتری است. در نمونه‌های بزرگ (۳۰ مشاهده و بیشتر) عملاً تفاوت کمی بین دو رابطه بالا در محاسبه واریانس به وجود می‌آید.

اگر ریشه مثبت واریانس را محاسبه کنیم، انحراف معیار به دست می‌آید. انحراف معیار جامعه با $\sigma$ و نمونه با $s$ نشان داده می‌شود:

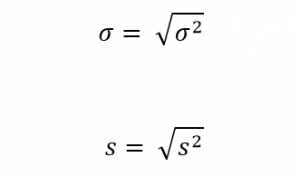انحراف معیار ازآن‌جهت اهمیت دارد که پایه‌ای است برای بیان درصدی از داده‌ها که در فاصله مشخصی از میانگین واقع‌شده‌اند. در بخش مباحث تکمیلی به این مسئله اشاره می‌کنم.

اگر همه داده‌ها مقدار برابری داشته باشند واریانس و انحراف معیار صفر خواهند بود. اگر به همه داده‌ها مقدار ثابتی اضافه یا کم شود، تغییری در واریانس و انحراف معیار ایجاد نمی‌کند. به شکل مفهومی نیز روشن است چراکه اضافه یا کم کردن یک عدد ثابت تغییری در نحوه پراکندگی داده‌ها ایجاد نمی‌کند بلکه داده‌ها را به‌اندازه مشخصی جابجا می‌کند.

در نرم‌افزار اکسل به ترتیب از توابع ()VAR.P و ()VAR.S برای محاسبه واریانس جمعیت و نمونه آماری استفاده می‌شود. برای محاسبه انحراف معیار توابع ()STDEV.P و ()STDEV.S بکار می‌روند. در مثال قبل خانه E6 حاوی فرمول زیر است:

VAR.S(C3:C22)=

در خانه E7 نیز از رابطه زیر برای محاسبه انحراف معیار استفاده شده است:

STDEV.S(C3:C22)=

در زبان R توابع ()var و ()sd برای محاسبه واریانس و انحراف معیار بکار می‌روند. توجه کنید که در هر دو تابع در مخرج کسر از $n-1$ استفاده می‌شود. من کد زیر را برای محاسبه این دو سنجه برای داده‌های مثال بکار بردم:

#Variance and Standard Deviation

var(Data$Weight.Ounces)

[1] 0.6840789

sd(Data$Weight.Ounces)

[1] 0.8270907

مباحث تکمیلی

قاعده چبیشف (Chebyshev’s Theorem)

وقتی انحراف معیار جامعه یا نمونه کوچک باشد، مقدار هر مشاهده نزدیک به میانگین قرار دارد. درحالی‌که اگر انحراف معیار بزرگ باشد، مشاهدات به شکل پراکنده‌تری حول میانگین توزیع شده‌اند. آماردان روسی، چبیشف، سعی کرد این پدیده را به شکل کمّی دربیاورد. قاعده چبیشف صرف‌نظر از این‌که توزیع داده‌ها چگونه باشد، یک کمینه برای درصدی از مشاهدات تعیین می‌کند که در فاصله مشخصی برحسب انحراف معیار از میانگین قرار دارند.

قاعده چبیشف بیان می‌کند در یک جامعه یا نمونه آماری، درصد مشاهداتی که در فاصله k برابر انحراف معیار از میانگین قرار دارند حداقل برابر مقدار زیر است ( $k>0$ ):

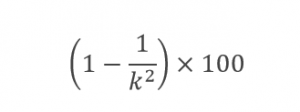
اگر بخواهیم این قاعده را برای داده‌های مثال بکار ببریم، با فرض k=2، مقدار بالا ۷۵ درصد خواهد شد. بر اساس قاعده چبیشف وزن حداقل ۷۵ درصد بسته‌های خروجی دستگاه ج در بازه زیر قرار می‌گیرد:

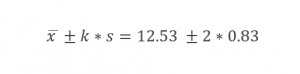قاعده تجربی

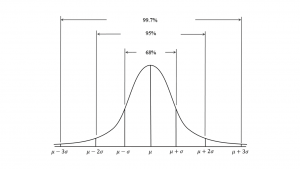
اگرچه قاعده چبیشف را می‌توان برای هر توزیعی با هر شکلی بکار برد، قوانین سرانگشتی زیر را تنها می‌توان برای توزیع‌هایی که دارای منحنی زنگوله‌ای و متقارن هستند، بکار برد (شکل-۴):

نزدیک ۶۸ درصد مشاهدات در فاصله ۱ برابر انحراف معیار از میانگین قرار می‌گیرند.

نزدیک ۹۵ درصد مشاهدات در فاصله ۲ برابر انحراف معیار از میانگین قرار می‌گیرند.

تقریباً تمام مشاهدات در فاصله ۳ برابر انحراف معیار از میانگین قرار می‌گیرند.

اگر فرض کنیم توزیع وزن بسته‌های خروجی از دستگاه ج دارای منحنی زنگوله‌ای و متقارن است، می‌توان گفت وزن ۹۵ درصد بسته‌ها در فاصله زیر قرار دارد:

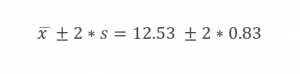توجه کنید این همان بازه‌ای است که از قاعده چبیشف به دست آمد. قاعده چبیشف بدون هیچ فرضی در مورد توزیع داده‌ها، حد پایینی را ۷۵ درصد برآورد می‌کند. با داشتن اطلاعات اضافی در مورد شکل توزیع داده‌ها، حال می‌توانیم بگوییم ۹۵ درصد داده‌ها در این فاصله قرار می‌گیرند.

استاندارد کردن داده

همان طور که در مقاله “فرآیند اجرای پروژه‌های داده‌کاوی” توضیح دادم یکی از روش های آماده سازی داده، نرمال یا استاندارد کردن است. استاندارد کردن به این معنی است که داده ها را براساس فاصله (برحسب انحراف معیار) از میانگین ارائه کنیم. برای هر مشاهده در نمونه، از رابطه زیر می توان آن را استاندارد کرد:

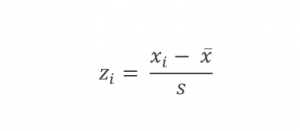ازآنجاکه داده‌ها ممکن است برحسب واحدهای مختلفی باشند، این کار کمک می‌کند همه داده‌ها بدون واحد شوند. برای نمونه سطح درآمد سالیانه مقدار عددی بسیار بزرگ‌تری از میزان تجربه برحسب سال را به خود می‌گیرد. این مسئله ممکن است در مدل‌های ریاضی سوگیری ایجاد کند. با استفاده از استاندارد کردن داده‌ها این مشکل را می‌توان برطرف نمود.

منابع:

Levine, D. M., Berenson, M. L., & Stephan, D. (1999). “Statistics for Managers Using Microsoft Excel”, Upper Saddle River, NJ: Prentice Hall

Weiers, R. M. (2010). “Introduction to Business Statistics”, Cengage Learning

12 نظر در “شاخص‌های پراکندگی در آمار”

شهاب شریفی
آذر ۱۹, ۱۳۹۸ در ۸:۵۲ ق٫ظ
پیوند یکتا
بسیار عالی بود
پاسخ
جواد
فروردین ۳۰, ۱۳۹۹ در ۴:۵۸ ب٫ظ
پیوند یکتا
متشکرم واقعا به زبان قابل فهم و روان بود
پاسخ
نوکنده
خرداد ۳۰, ۱۳۹۹ در ۱:۰۴ ق٫ظ
پیوند یکتا
بسیار عالی توضیح دادین ممنون از زحماتتون
پاسخ
شیوا
شهریور ۲, ۱۳۹۹ در ۸:۱۲ ب٫ظ
پیوند یکتا
ممنون از توضیحات عالی تون
پاسخ
مهربان
دی ۱۷, ۱۳۹۹ در ۱۱:۵۳ ق٫ظ
پیوند یکتا
متشکر از بیان خوب وتوضیح دقیق
پاسخ
مهربان
دی ۱۷, ۱۳۹۹ در ۱۲:۰۶ ب٫ظ
پیوند یکتا
متشکر ایکاش جدول انحراف معیار را نسبت به تلرانس های مورد قبول را بعنوان پیش فرض تهیه می نمود
پاسخ
رسولق
بهمن ۹, ۱۳۹۹ در ۷:۲۸ ق٫ظ
پیوند یکتا
خیلی خوب و عالی توضیح داده بودید
تشکر
پاسخ
زهرا
فروردین ۱۹, ۱۴۰۰ در ۹:۳۵ ق٫ظ
پیوند یکتا
ممنون از توضیحات عالی
پاسخ
فاطمه
خرداد ۱۹, ۱۴۰۰ در ۳:۲۲ ب٫ظ
پیوند یکتا
عالی بود متشکرم
پاسخ
علیرضا آفریده
آذر ۲۶, ۱۴۰۰ در ۹:۴۶ ب٫ظ
پیوند یکتا
واقعا عالی بود انشاا… موفق باشید .
پاسخ
امين
دی ۲۶, ۱۴۰۰ در ۹:۵۰ ب٫ظ
پیوند یکتا
من زمانی که دانشجو بودم تحلیل یک ۹ گرفتم رفتم خدمت استاد که ۹ ۱۰ میشه یا نه گفت نه و افتادم ترم بعد رفتم تحلیل یک بردارم دیدم یکی از اساتید درس رو برداشته که همه ازش میترسیدن و نمی گرفتن درس رو باهاش چون میگفتن همه می افتن من کار میکردم و زمانهام نمی خورد مجبور شدم با اون بردارم تحلیل یک رو
جلسه اول که رفتم سر کلاس گفت حضور و غیاب ندارم و هرکسی اومد اومد ولی انقدر خوب درس داد که من تازه فهمیدم استاتیک و مقاومت هیچی بلد نیستم و همین باعث شد کل کلاسهاش رو که دقیقا ۲ ساعت رو درس میداد از اول کلاس تا اخرش بشینم و هیچ غیبت هم نداشتم اخر ترم شدم نمره دوم کلاسش ۱۴
اما واقعا در زندگی ام از افتادنهایی هست که حسابی ازش راضی ام
امروز سایت شما رو که خوندم حس درس دادن اون استاد بهم دست داد خیلی عالی و عینی توضیح دادید
به سهم خودم سپاسگذارم
پاسخ
- فرزاد مینویینویسنده مطلب
  دی ۲۶, ۱۴۰۰ در ۱۰:۲۲ ب٫ظ
  پیوند یکتا
  سلام و عرض ادب،
  از بازخورد شما خیلی سپاسگزارم و مایه قوت قلب بود.
  پاسخ

آنالیکا