بررسی نرمال بودن داده‌ها

می‌توان گفت توزیع نرمال (Normal Distribution) یکی از پرکاربردترین توزیع‌های احتمالی در آمار و یادگیری ماشین است. علاوه بر این توزیع نرمال در توصیف خروجی بسیاری از فرآیندهای تصادفی در دنیای واقعی هم بسیار مفید است. در این مقاله بحث می‌کنم چگونه تشخیص دهید یک نمونه داده از جمعیتی با توزیع نرمال آمده است و چطور این مراحل را در نرم‌افزار R و پایتون پیاده کنید. قبل از آن مروری بر ویژگی‌های توزیع نرمال به فهم بحث کمک می‌کند.

ویژگی‌های توزیع نرمال

برای به دست آوردن توزیع نرمال، کافی است تنها میانگین و انحراف معیار توزیع را داشته باشید. برای مثال شکل-۱، نمونه یک توزیع نرمال با میانگین ۱۰ و انحراف معیار ۱ را نشان می‌دهد.

توزیع نرمال یک توزیع متقارن است بنابراین شاخص چولگی آن صفر است. شاخص کشیدگی توزیع نرمال ۳ است. در این توزیع میانگین در وسط توزیع است و میانگین، میانه و مد داده‌ها همگی باهم برابر هستند. دنباله‌های توزیع نرمال از منفی بی‌نهایت تا مثبت بی‌نهایت امتداد دارند و گرچه به صفر میل می‌کنند ولی هیچ‌گاه محور افقی را قطع نمی‌کنند.

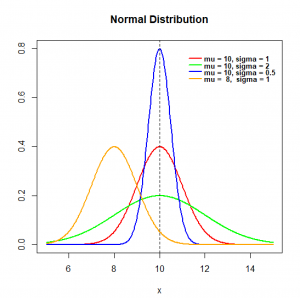
همان‌طور که اشاره شد توزیع نرمال با دو پارامتر میانگین و انحراف معیار به‌طور کامل به دست می‌آید. در شکل-۲ اثرات تغییرات پارامتر میانگین (mu) و انحراف معیار (sigma) را بر روی توزیع نرمال مشاهده می‌کنید. هرچه انحراف معیار بزرگ‌تر شود، داده‌ها حول میانگین پراکنده‌تر هستند. تغییر در میانگین نیز مرکزیت داده‌ها را جابجا می‌کند.

آزمون نرمال بودن داده‌ها

در بسیاری از کاربردها در آمار یا یادگیری ماشین نیاز است فرض نرمال بودن بررسی شود. برای مثال، در آزمون t برای مقایسه میانگین دو گروه، فرض این است که داده‌ها از جمعیتی با توزیع نرمال آمده‌اند. یا در رگرسیون خطی، فرض این است خطاهای مدل از توزیع نرمال با میانگین صفر و انحراف معیار ثابت پیروی می‌کنند. بنابراین ممکن است در مراحل تحلیل داده نیاز باشد که چنین فرضی را بررسی کنید.

فرآیندی که من پیشنهاد می‌دهم یک فرآیند سه مرحله‌ای است که شما گام‌به‌گام فرض نرمال بودن داده‌ها را در جامعه بررسی می‌کنید. من این فرآیند را از دکتر رِی لیتل جان (Ray Littlejohn) استاد درس آمار کاربردی در دانشگاه کلرادو آمریکا (University of Colorado, Boulder, USA) الهام گرفتم. من این فرآیند را در تحلیل داده‌های مختلف بکار برده‌ام و فکر می‌کنم بسیار مفید است. به همین خاطر توصیه می‌کنم شما هم‌ چنین فرآیندی را استفاده کنید.

قبل از آن توجه کنید، هدف از چنین فرآیندی این است که بر اساس نمونه داده‌های در دسترس به استنباطی از توزیع واقعی داده‌ها از جامعه برسیم. این همان رویکردی است که در آمار استنباطی (Inferential Statistics) دنبال می‌شود. ما نمی‌توانیم اثبات کنیم که جامعه از توزیع نرمال پیروی می‌کند بلکه تنها می‌توانیم فرض نرمال بودن داده‌ها را در جامعه رد کنیم.

برای آنکه من این فرآیند را نشان دهم، در R هزار عدد تصادفی از توزیع گاما (Gamma Distribution) با پارامترهای shape = 1 و rate = 1 ایجاد کردم و آن را در بردار x ذخیره کردم. شما می‌توانید هر داده دیگری را به‌جای x بکار ببرید.

#Create a sample data
set.seed(1234)
x <- rgamma(1000, shape = 1, rate = 1)

#Create a sample data

set.seed(1234)

x <- rgamma(1000, shape = 1, rate = 1)

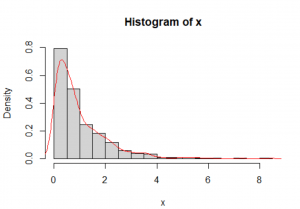
در گام اول، بهتر است به‌صورت کیفی هیستوگرام داده‌ها را رسم کنید و تابع توزیع چگالی احتمال برآوردشده را روی آن بیندازید. هدف این است به‌صورت چشمی بررسی کنید چقدر تابع توزیع چگالی احتمال برآوردشده به توزیع نرمال نزدیک است. گرچه این روش چشمی است و بسته به تجربیات قبلی شما در تحلیل داده دارد، ولی انحراف‌های مشخص از توزیع نرمال به‌سرعت خود را نشان می‌دهد. برای مثالی که زدم، شکل-۳ به‌خوبی نشان می‌دهد داده‌های ما چولگی شدیدی به سمت راست دارند و بعید است که این داده‌ها از جامعه‌ای با توزیع نرمال آمده باشند.

#Test of Normality
#Histogram
hist(x, probability = T, breaks = 15)
lines(density(x), col = "red")

#Test of Normality

#Histogram

hist(x, probability = T, breaks = 15)

lines(density(x), col = "red")

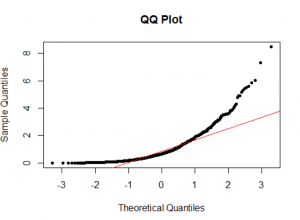
در گام دوم، نمودار چندک-چندک (Q-Q Plot) و مقایسه آن با خط ۴۵ درجه (خط قرمزرنگ) است. اگر با مفهوم این نمودار آشنا نیستید، نیاز است مقاله “نمودار چندک-چندک چیست و چه کاربردی دارد؟” را مطالعه کنید. این روش هم یک رویکرد توصیفی است و شما با چشم میزان انحراف داده‌ها از خط ۴۵ درجه را بررسی می‌کنید. هرچه داده‌ها از خط ۴۵ درجه انحراف بیشتری داشته باشند، می‌توانید فرض نرمال بودن داده‌ها در جامعه را قوی‌تر رد کنید. برای مثالی که زدم، شکل-۴ انحراف‌های جدی نسبت به خط ۴۵ درجه را نشان می‌دهد. پس این رویکرد هم فرض نرمال بودن داده‌ها را در جامعه رد می‌کند. این رویکرد گرچه توصیفی است، ولی چون شما نتایج را با یک خط معیار مقایسه‌ای می‌کنید، حتی اگر تجربه زیادی هم در تحلیل داده نداشته باشید، می‌توانید از آن به‌خوبی استفاده کنید.

#QQ-plot
qqnorm(x, main = "QQ Plot", pch = 20)
qqline(x, col = "red")

#QQ-plot

qqnorm(x, main = "QQ Plot", pch = 20)

qqline(x, col = "red")

در گام سوم، از آزمون‌های آماری که برای بررسی نرمال بودن داده‌ها توسعه یافته‌اند، استفاده کنید. در آمار آزمون‌های گوناگونی مانند آزمون اندرسون-دارلینگ (Anderson-Darling)، آزمون شاپیرو-ویلک (Shapiro-Wilk Test)، آزمون کولموگروف–اسمیرنف (Kolmogorov–Smirnov Test)، آزمون لین- مودهالکار (Lin-Mudholkar Test) و آزمون‌های گشتاور (Moments Test) وجود دارد.

بر اساس مرور ادبیات آمار، من پیشنهاد می‌کنم وقتی اندازه نمونه شما کوچک است (نمونه ۲۵ تایی یا کمتر) از آزمون شاپیرو-ویلک استفاده کنید. فرض صفر (H0) در آزمون شاپیرو-ویلک این است داده‌ها از جامعه با توزیع نرمال آمده است. اگر مقدار p آزمون آماری از ۰٫۰۵ کوچک‌تر شد، فرض صفر رد می‌شود. اگر مقدار p آزمون آماری از ۰٫۰۵ بزرگ‌تر شد، نمی‌توانیم این فرض را رد کنیم که داده‌ها از توزیع نرمال آمده‌اند. پس تا پیدا شدن شواهد جدید، می‌پذیریم داده‌ها از جامعه‌ای با توزیع نرمال آمده‌اند.

آزمون شاپیرو-ویلک، در بیشتر مواقع نسبت به آزمون اندرسون-دارلینگ و آزمون کولموگروف–اسمیرنف توان آماری (Power) بالاتری دارد. توان آماری یک آزمون، احتمال آن است که وقتی فرضیه صفر در واقعیت غلط است، آن را به‌درستی رد کنید.

اگر بخواهید در R، این آزمون را انجام دهید از تابع shapiro.test استفاده کنید. در این مثال اندازه نمونه بزرگ‌تر از ۲۵ است و بهتر است از این آزمون استفاده نکنید. وقتی اندازه نمونه بزرگ‌تر از ۲۵ است، استفاده از این آزمون ممکن است منجر به رد H0 شود، درحالی‌که H0 درست باشد. من در اینجا فقط برای آنکه یاد بگیرید چگونه این کار را انجام دهید، روی ‌داده‌های مثالی که زدم، آن را اجرا می‌کنم.

#Shapiro-Wilk Test for Normality 
#p-value < 0.05 reject normality assumption
#Good for sample size <= 25
shapiro.test(x)


Shapiro-Wilk normality test

data:  x
W = 0.79946, p-value < 2.2e-16

#Shapiro-Wilk Test for Normality

#p-value < 0.05 reject normality assumption

#Good for sample size <= 25

shapiro.test(x)

Shapiro-Wilk normality test

data: x

W = 0.79946, p-value < 2.2e-16

همان‌طور که مشخص است مقدار p عدد بسیار کوچکی و نزدیک به صفر است. پس فرض H0 را رد می‌کنم و نمی‌توانم بپذیرم این داده‌ها از جامعه‌ای با توزیع نرمال آمده است.

اگر اندازه نمونه بزرگ‌تر از ۲۵ باشد، بهتر است از آزمون‌های گشتاور استفاده کنید. دو آزمون چولگی (Skewness Test) و کشیدگی (Kurtosis Test) برای این منظور بکار می‌رود.

در آزمون چولگی که به آزمون جارکی-برا (Jarque-Bera Test) هم معروف است، فرض صفر این است که داده‌ها از توزیعی با چولگی صفر (همان چولگی توزیع نرمال) آمده‌اند. اگر مقدار p آزمون آماری از ۰٫۰۵ کوچک‌تر شد، فرض H0 رد می‌شود.

در آزمون کشیدگی که به آزمون انسکوم-گلین (Anscombe-Glynn Test) هم معروف است، فرض صفر این است که داده‌ها از توزیعی با کشیدگی ۳ (همان کشیدگی توزیع نرمال) آمده‌اند. اگر مقدار p آزمون آماری از ۰٫۰۵ کوچک‌تر شد، فرض H0 رد می‌شود.

در R برای انجام این دو آزمون، لازم است از کتابخانه Moments استفاده کنید. توابع jarque.test و anscombe.test از این کتابخانه به ترتیب آزمون‌های چولگی و کشیدگی را انجام می‌دهند.

#Call Moments Library
library(moments)

#Jarque-Bera Test (Skewness = 0 ?)
#p-value < 0.05 reject normality assumption
jarque.test(x)


	Jarque-Bera Normality Test

data:  x
JB = 2862.1, p-value < 2.2e-16
alternative hypothesis: greater

#Anscombe-Glynn Test (Kurtosis = 3 ?)
#p-value < 0.05 reject normality assumption
anscombe.test(x)

Anscombe-Glynn kurtosis test

data:  x
kurt = 10.081, z = 12.277, p-value <
2.2e-16
alternative hypothesis: kurtosis is not equal to 3

#Call Moments Library

library(moments)

#Jarque-Bera Test (Skewness = 0 ?)

#p-value < 0.05 reject normality assumption

jarque.test(x)

Jarque-Bera Normality Test

data: x

JB = 2862.1, p-value < 2.2e-16

alternative hypothesis: greater

#Anscombe-Glynn Test (Kurtosis = 3 ?)

#p-value < 0.05 reject normality assumption

anscombe.test(x)

Anscombe-Glynn kurtosis test

data: x

kurt = 10.081, z = 12.277, p-value <

2.2e-16

alternative hypothesis: kurtosis is not equal to 3

همان‌طور که مشخص است نتایج هر دو آزمون، مقدار p کوچک‌تر از ۰٫۰۵ می‌دهند. پس فرض H0 را رد می‌کنم.

بنابراین جمع‌بندی نهایی من این است که این داده‌ها از جامعه‌ای با توزیع نرمال نیامده‌اند. البته در این مثال، ما می‌دانیم که من این داده‌ها را از توزیع گاما ایجاد کردم و بر اساس نتایج کار به‌درستی فرض نرمال بودن داده‌ها در جامعه رد شد. اگر تمایل دارید پیاده‌سازی این سه ‌گام را پایتون ببینید، من کدهای آن را در بخش ضمیمه آورده‌ام.

جمع‌بندی

در این مقاله من یک فرآیند سه مرحله‌ای را برای بررسی نرمال بودن داده‌ها در جامعه بر اساس نمونه پیشنهاد دادم:

گام اول، رسم هیستوگرام و تابع توزیع چگالی احتمال برآوردشده و مقایسه چشمی آن با توزیع نرمال،

گام دوم، رسم نمودار Q-Q Plot و مقایسه داده‌ها با خط معیار،

گام سوم، انجام آزمون‌های آماری،

اگر اندازه نمونه از ۲۵ کوچک‌تر است، آزمون شاپیرو-ویلک را انجام دهید.

اگر اندازه نمونه از ۲۵ بزرگ‌تر است، آزمون‌های چولگی و کشیدگی را انجام دهید.

از نتایج این سه مرحله، درباره پذیرفتن فرض نرمال بودن داده‌ها در جامعه قضاوت کنید.

***ضمیمه: بررسی نرمال بودن داده‌ها در پایتون

در این بخش همان مراحلی که در R، اجرا کردم را در پایتون پیاده‌سازی کردم.

در ابتدا پس از فراخوانی کتابخانه‌های لازم، هزار عدد تصادفی از توزیع گاما با پارامترهای shape = 1 و rate = 1 ایجاد کردم و آن را در بردار x ذخیره کردم. شما می‌توانید هر داده دیگری را به‌جای x بکار ببرید.

#Required Libraries
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api 

#Create a sample data
np.random.seed(123)
x = np.random.gamma(shape = 1.0, scale = 1.0, size = 1000)

#Required Libraries

import numpy as np

import matplotlib.pyplot as plt

import seaborn as sns

import statsmodels.api

#Create a sample data

np.random.seed(123)

x = np.random.gamma(shape = 1.0, scale = 1.0, size = 1000)

در گام اول، هیستوگرام داده‌ها را رسم کردم و تابع توزیع چگالی احتمال برآوردشده را روی آن انداختم. نتایج در شکل-۵ آمده است.

#Test of Normality
#Histogram
sns.histplot(x, stat = 'density', fill = False, color = 'gray')
sns.kdeplot(x, color = "red")
plt.title('Histogram of x')

#Test of Normality

#Histogram

sns.histplot(x, stat = 'density', fill = False, color = 'gray')

sns.kdeplot(x, color = "red")

plt.title('Histogram of x')

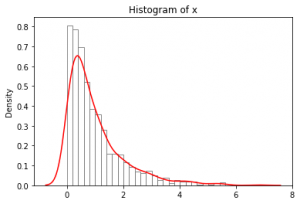
در گام دوم، نمودار چندک-چندک (Q-Q Plot) را رسم کردم و داده‌ها را با خط معیار (خط قرمزرنگ) مقایسه کردم (شکل-۶).

#QQ-plot
statsmodels.qqplot(x, line = 's')

1 2	#QQ-plot statsmodels.qqplot(x, line = 's')

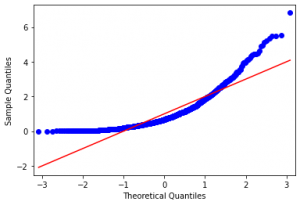
در گام سوم، از آزمون‌های آماری متناسب برای بررسی نرمال بودن داده‌ها استفاده کردم.

اگر اندازه نمونه کوچک‌تر از ۲۵ باشد، از آزمون‌ شاپیرو-ویلک به طریق زیر استفاده کنید.

#Shapiro-Wilk Test for Normality 
#p-value < 0.05 reject normality assumption
#Good for sample size <= 25
from scipy.stats import shapiro
shapiro(x)


ShapiroResult(statistic=0.8131569027900696, pvalue=1.7153733391528338e-32)

#Shapiro-Wilk Test for Normality

#p-value < 0.05 reject normality assumption

#Good for sample size <= 25

from scipy.stats import shapiro

shapiro(x)

ShapiroResult(statistic=0.8131569027900696, pvalue=1.7153733391528338e-32)

اگر اندازه نمونه بزرگ‌تر از ۲۵ باشد، آزمون‌های گشتاور را به طریق زیر انجام دهید.

#Jarque-Bera Test (Skewness = 0 ?)
#p-value < 0.05 reject normality assumption
from scipy.stats import jarque_bera
jarque_bera(x)

Jarque_beraResult(statistic=1340.5914063908351, pvalue=0.0)

#Anscombe-Glynn Test (Kurtosis = 3 ?)
#p-value < 0.05 reject normality assumption
from scipy.stats import kurtosistest
kurtosistest(x)

KurtosistestResult(statistic=10.156711893142147, pvalue=3.0933309713991858e-24)

#Jarque-Bera Test (Skewness = 0 ?)

#p-value < 0.05 reject normality assumption

from scipy.stats import jarque_bera

jarque_bera(x)

Jarque_beraResult(statistic=1340.5914063908351, pvalue=0.0)

#Anscombe-Glynn Test (Kurtosis = 3 ?)

#p-value < 0.05 reject normality assumption

from scipy.stats import kurtosistest

kurtosistest(x)

KurtosistestResult(statistic=10.156711893142147, pvalue=3.0933309713991858e-24)

منابع:

Field, A., Miles, J., & Field, Z. (2012). “Discovering Statistics Using R”. SAGE Publications Ltd

Littlejohn, R. (2014), “Introduction to Applied Statistical Methods” – Course Material, University of Colorado, Boulder, USA

Razali, N., Wah, Y. B. (2011). “Power Comparisons of Shapiro–Wilk, Kolmogorov–Smirnov, Lilliefors and Anderson–Darling Tests”, Journal of Statistical Modeling and Analytics, 2(1)

2 نظر در “بررسی نرمال بودن داده‌ها”

سامان
آذر ۲۹, ۱۴۰۰ در ۱۰:۱۶ ب٫ظ
پیوند یکتا
سلام استاد عزیز، آقای مینویی
مدتی هست که دلمون برای شما تنگ شده و در تلگرام هم پیداتون نکردم جویای حال شما باشم
امیدوارم هر جا که هستید شاد و سلامت باشید
پاسخ
- فرزاد مینویینویسنده مطلب
  دی ۷, ۱۴۰۰ در ۹:۰۸ ب٫ظ
  پیوند یکتا
  سلام سامان جان،
  خیلی لطف کردی اینجا پیام گذاشتی. امیدوارم همیشه سلامت و شاد باشی. من در تلگرام در آیدی زیر هستم:
  FarzadMinooei01
  پاسخ

آنالیکا

بررسی نرمال بودن داده‌ها

ویژگی‌های توزیع نرمال

آزمون نرمال بودن داده‌ها

جمع‌بندی

***ضمیمه: بررسی نرمال بودن داده‌ها در پایتون

2 نظر در “بررسی نرمال بودن داده‌ها”

دیدگاهتان را بنویسید لغو پاسخ