نمودار چندک-چندک (Q-Q Plot) چیست و چه کاربردی دارد؟

نمودار چندک-چندک (Quantile-Quantile Plot) یک ابزار توصیفی است که کمک می‌کند بفهمیم یک مجموعه داده از یک توزیع احتمالی مشخص مانند توزیع نرمال (Normal Distribution) یا نمایی (Exponential Distribution) پیروی می‌کند یا خیر. برای مثال فرض نرمال بودن داده‌ها در بسیاری از آزمون‌های آماری وجود دارد. بنابراین قبل از انجام چنین آزمون‌های آماری نیاز است تا بررسی کنیم که داده‌ها از توزیع نرمال پیروی می‌کند. یک ابزار ساده و قدرتمند در چنین تحلیلی، استفاده از نمودار چندک-چندک است.

درک شهودی نمودار چندک-چندک

این نمودار با رسم چندک‌های دو توزیع در مقابل یکدیگر به دست می‌آید. برای فهم شهودی این نمودار به مثال زیر توجه کنید.

فرض کنید یک نمونه ۱۵ تایی داده به شکل زیر داریم:

۴۰٫۸ ۲۴٫۵ ۴۶٫۱

۱۷٫۲ ۱۹٫۷ ۳۳٫۲

۲۶٫۷ ۱۸٫۶ ۴۳٫۳

۳۷٫۲ ۴۴٫۸ ۳۱٫۴

۲۵٫۶ ۲۷٫۶ ۱۱٫۶

برای این داده‌ها می‌توان میانه (Median) را محاسبه کرد. میانه یک شاخص مرکزی است. اگر داده‌ها به ترتیب از کوچک‌تر به بزرگ‌تر مرتب شوند، نیمی از آن‌ها از میانه کوچک‌تر و نیمی دیگر از میانه بزرگ‌تر هست. اگر تعداد اعداد فرد باشد، عدد وسطی میانه است. اگر تعداد زوج باشد میانه برابر میانگین دو عدد وسطی خواهد بود. به‌این‌ترتیب میانه، داده‌ها را به دو قسمت تقسیم می‌کند . پنجاه‌درصد داده‌ها از میانه کوچک‌تر و پنجاه‌درصد داده‌ها از آن بزرگ‌تر هستند. به همین دلیل به میانه چندک ۵۰ درصد (Q50%) یا چارک دوم هم گفته می‌شود.

این ایده را می‌توان تعمیم داد. به‌این‌ترتیب که در بخش ۵۰ درصد اول (اعدادی که از میانه کوچک‌ترند)، دوباره عددی را پیدا کرد که داده‌ها را به دو بخش با تعداد مساوی تقسیم می‌کند. به این عدد چارک اول یا چندک ۲۵ درصد (Q25%) گفته می‌شود.

به‌طور مشابه در آن بخش از داده‌ها که از میانه بزرگ‌تر هستند نیز می‌توان عددی را پیدا کرد که داده‌ها را به دو قسمت مساوی تقسیم کند. به این عدد چارک سوم یا چندک ۷۵ درصد (Q75%) می‌گویند. به‌این‌ترتیب چارک‌ها داده‌ها را به چهار قسمت برابر تقسیم می‌کنند. شکل-۱ این مفهوم را برای مثال بالا نشان می‌دهد.

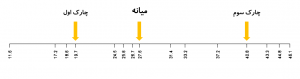
گرچه چارک‌ها (Quantiles) در آمار بسیار کاربردی هستند، می‌توان فکر کرد می‌شود این ایده را بازهم تعمیم داد. مثلاً چرا چندک ۲۰ درصد نداشته باشیم؟ یا چرا چندک ۱۰ درصد نداشته باشیم؟ می‌توان این ایده را همان‌طور ادامه داد تا اینکه همه مقادیر داده خودشان چندک شوند. شکل–۲ چنین ایده‌ای را نشان می‌دهد.

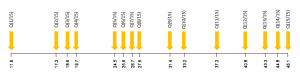
برای مثال عدد ۱۷٫۲ جایی است که ۲/۱۵ یا حدود ۱۳ درصد داده‌ها از آن کوچک‌تر یا مساوی هستند. پس ۱۷٫۲ چندک ۱۳ درصد است. به‌این‌ترتیب این چندک‌ها داده‌ها را به بخش‌های مساوی تقسیم می‌کنند.

این ایده را می‌توان برای هر توزیع داده‌ای ازجمله توزیع نرمال استاندارد (Standard Normal Distribution) توسعه داد. در شکل-۳ مشاهده می‌کنید که ۱۵ چندک که داده‌های توزیع نرمال استاندارد را به بخش‌های مساوی تقسیم می‌کنند، نشان داده شده است. توجه کنید توزیع نرمال استاندارد دارای میانگین صفر و انحراف معیار ۱ است. هر توزیع نرمال با میانگین و انحراف معیار دلخواه را می‌توان به توزیع نرمال استاندارد تبدیل کرد. برای مطالعه بیشتر، به بخش استاندارد کردن مقاله “شاخص‌های پراکندگی در آمار” مراجعه کنید.

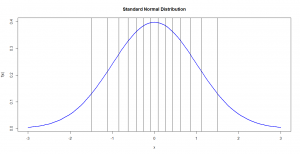
در نمودار بالا توجه کنید چون تراکم داده‌ها حول میانگین بیشتر است، فاصله چندک‌ها از یکدیگر در مرکز داده‌ها کمتر است. در مقابل چون تراکم داده‌ها در دو انتهای توزیع کم می‌شود هرچه از مرکز توزیع دورتر می‌شویم، فاصله بین چندک‌ها بیشتر می‌شود.

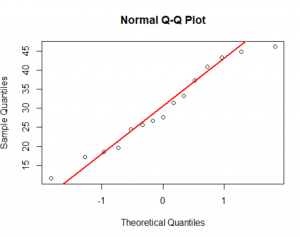
نمودار Q-Q، پانزده چندک در نمونه‌ داده‌ها را در مقابل پانزده چندک توزیع نرمال رسم می‌کند (شکل-۴). محور عمودی، هریک از چندک‌ها در نمونه و محور افقی، همان چندک‌ها در توزیع نرمال استاندارد را نشان می‌دهد. اگر نمونه داده‌ها از توزیع نرمال پیروی کند، باید داده‌ها نزدیک به خط ۴۵ درجه (خط قرمزرنگ) باشند. در این مثال می‌بینید که با تقریب خوبی نقاط به خط ۴۵ درجه نزدیک هستند. بنابراین نتیجه می‌گیریم داده‌ها از توزیع نرمال پیروی می‌کنند.

این همان کاری است که وقتی شما با چشم نمودارهای دو توزیع را مقایسه می‌کنید، به‌صورت شهودی انجام می‌دهید. در شکل-۵ من دو توزیع رسم کردم. فرض کنید توزیع ۱ از توزیع نرمال پیروی می‌کند و می‌خواهید توزیع ۲ را با آن مقایسه کنید. با چشم مشخص است که بعید است توزیع ۲ از توزیع نرمال آمده باشد. وقتی به چندک ۱۰ درصد دو توزیع نگاه می‌کنید در تناظر باهم قرار ندارند. چراکه در توزیع ۱ ما تراکم زیادی از داده‌ها را در سمت چپ نمودار داریم بنابراین چندک ۱۰ درصد بیشتر متمایل به سمت چپ است. ولی در توزیع نرمال که در انتهای توزیع تراکم کمی از داده‌ها داریم، چندک ۱۰ درصد از دم انتهایی سمت چپ فاصله بیشتری دارد. عملاً شما به‌صورت شهودی چندک‌های مختلفی را باهم بررسی می‌کنید تا به این جمع‌بندی برسید که آیا توزیع دو نمونه باهم یکسان است یا خیر.

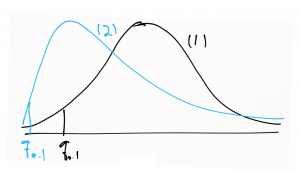
مزیت استفاده از نمودار Q-Q نسبت به مقایسه توزیع چگالی، این است که آن را می‌توان با خط ۴۵ درجه مقایسه کرد و راحت‌تر تصمیم گرفت. ولی در هر شکل توجه کنید این تنها یک روش توصیفی است و معمولاً من در کارهایم از آزمون‌های آماری علاوه بر نمودار Q-Q هم استفاده می‌کنم.

مزیت دیگر استفاده از نمودار Q-Q این است که استفاده از آن تنها محدود به مقایسه با توزیع نرمال نیست و برای مقایسه با هر توزیع احتمالی دیگر می‌توان استفاده کرد.

رسم Q-Q Plot در R

استفاده از Q-Q Plot در R برای مقایسه توزیع نمونه با توزیع نرمال

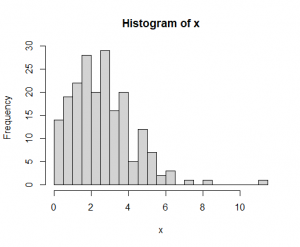
در این مثال من برداری مانند x با ۲۰۰ درایه ایجاد کردم که درایه‌های آن به‌صورت تصادفی از توزیع ویبول (Weibull) با پارامترهای shape = 1.5 و scale = 3 به‌دست‌آمده‌اند. توجه کنید x می‌تواند هر نمونه داده‌ای باشد. هیستوگرام داده‌ها در شکل-۶ آمده است. برای رسم نمودار چندک-چندک و مقایسه با توزیع نرمال استاندارد کافی است از تابع qqnorm در R استفاده کردم.

> #Create Synthetic Data
> set.seed(123)
> x <- rweibull(200, shape = 1.5, scale = 3)
> #Plot Histogram of x
> hist(x, breaks = 25)
> #Q-Q Plot
> qqnorm(x)
> qqline(x, col = 'red', lwd = 2)

> #Create Synthetic Data

> set.seed(123)

> x <- rweibull(200, shape = 1.5, scale = 3)

> #Plot Histogram of x

> hist(x, breaks = 25)

> #Q-Q Plot

> qqnorm(x)

> qqline(x, col = 'red', lwd = 2)

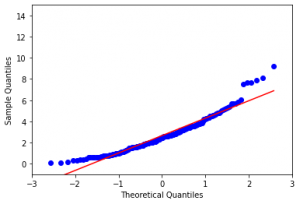
در اینجا ما می‌دانیم داده‌ها از توزیع ویبول آمده است پس بنابراین انتظار نداریم نمودار Q-Q روی خط ۴۵ درجه بیفتد. همان‌طور که شکل-۷ نشان می‌دهد، به‌خصوص در دو انتها، انحراف قابل‌توجهی از توزیع نرمال وجود دارد.

استفاده از Q-Q Plot در R برای مقایسه توزیع نمونه با توزیع دلخواه

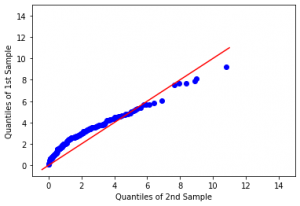
اگر من بخواهم توزیع x را با یک توزیع دلخواه دیگری مانند توزیع نمایی با پارامتر rate = 0.5 مقایسه کنم، کافی است از تابع qqplot استفاده کنم. آرگومان اول تعداد زیادی عدد تصادفی (مثلاً ۵۰۰ تا، بهتر است بیشتر از اندازه نمونه باشد) از توزیع موردنظر (در اینجا توزیع نمایی است) که با تابع rexp ایجاد کردم. آرگومان دوم این تابع، داده‌های نمونه است. شکل-۸ نشان می‌دهد که نمونه داده‌ها از توزیع نمایی با پارامتر rate = 0.5 فاصله زیادی دارد.

#Q-Q Plot
set.seed(123)
qqplot(rexp(500, rate = 0.5), x)
qqline(x, distribution = function(p) qexp(p, rate = 0.5), col = 'red', lwd = 2)

#Q-Q Plot

set.seed(123)

qqplot(rexp(500, rate = 0.5), x)

qqline(x, distribution = function(p) qexp(p, rate = 0.5), col = 'red', lwd = 2)

رسم Q-Q Plot در پایتون

استفاده از Q-Q Plot در پایتون برای مقایسه توزیع نمونه با توزیع نرمال

در پایتون من آرایه‌ای مانند x با ۲۰۰ درایه ایجاد کردم که درایه‌های آن به‌صورت تصادفی از توزیع ویبول (Weibull) با پارامترهای shape = 1.5 و scale = 3 به‌دست‌آمده‌اند. توجه کنید x می‌تواند هر نمونه داده‌ای باشد. در پایتون برای رسم نمودار چندک-چندک و مقایسه با توزیع نرمال استاندارد از کتابخانه statsmodels استفاده کردم.

#Required Libraries
import numpy as np
import statsmodels.api 
import matplotlib.pyplot as plt

#Create Synthetic Data
np.random.seed(123)
x = 3 * np.random.weibull(1.5, size = 200) #scale = 3, shape = 1.5

#Histogram of Data
plt.hist(x, bins = 15)

#QQ-plot (Comparing w/ Normal Distribution)
statsmodels.graphics.gofplots.qqplot(x, line = 's')
plt.xlim(-3, 3)
plt.ylim(-1, 15)

#Required Libraries

import numpy as np

import statsmodels.api

import matplotlib.pyplot as plt

#Create Synthetic Data

np.random.seed(123)

x = 3 * np.random.weibull(1.5, size = 200) #scale = 3, shape = 1.5

#Histogram of Data

plt.hist(x, bins = 15)

#QQ-plot (Comparing w/ Normal Distribution)

statsmodels.graphics.gofplots.qqplot(x, line = 's')

plt.xlim(-3, 3)

plt.ylim(-1, 15)

در اینجا ما می‌دانیم داده‌ها از توزیع ویبول آمده است پس بنابراین انتظار نداریم نمودار Q-Q روی خط ۴۵ درجه بیفتد. همان‌طور که شکل-۹ نشان می‌دهد، به‌خصوص در دو انتها، انحراف قابل‌توجهی از توزیع نرمال وجود دارد.

استفاده از Q-Q Plot در پایتون برای مقایسه توزیع نمونه با توزیع دلخواه

اگر من بخواهم توزیع x را با یک توزیع دلخواه دیگری مانند توزیع نمایی با پارامتر rate = 0.5 مقایسه کنم، کافی است از تابع qqplot_2sample در کتابخانه statsmodels استفاده کنم. آرگومان اول این تابع را داده‌های نمونه و آرگومان دوم تعداد زیادی عدد تصادفی (مثلاً ۵۰۰ تا، بهتر است بیشتر از اندازه نمونه باشد) از توزیع موردنظر (در اینجا توزیع نمایی است) قرار دادم. برای ایجاد عدد تصادفی از توزیع نمایی با پارامتر rate = 0.5 در کتابخانه numpy از تابع exponential استفاده کردم. شکل-۱۰ نشان می‌دهد که نمونه داده‌ها از توزیع نمایی با پارامتر rate = 0.5 فاصله زیادی دارد.

#QQ Plot (Comparing w/ Exponential Distribution)
np.random.seed(123)
statsmodels.graphics.gofplots.qqplot_2samples(x, np.random.exponential(scale = 2, size = 500), line = '45')
plt.xlim(-1, 15)
plt.ylim(-1, 15)

#QQ Plot (Comparing w/ Exponential Distribution)

np.random.seed(123)

statsmodels.graphics.gofplots.qqplot_2samples(x, np.random.exponential(scale = 2, size = 500), line = '45')

plt.xlim(-1, 15)