عدم قطعیت در تصمیم‌گیری واقعاً چه معنا می‌دهد؟

بسیاری از تصمیماتی که در دنیای واقعی با آن مواجه هستیم همراه با ریسک یا عدم قطعیت است (در این متن ریسک و عدم قطعیت بجای هم بکار می‌روند، گرچه در متون تخصصی‌تر بین این دو فرق گذاشته می‌شود). اما من فکر می‌کنم بسیاری از ما در برخورد با ریسک واکنش‌های مناسبی از خود نشان نمی‌دهیم و یا حتی به شکل انفعالی با آن برخورد می‌کنیم. هدف من از این مقاله این است تا درک عمیق‌تری نسبت به عدم قطعیت به خواننده منتقل کنم. به‌طور مشخص به دنبال پاسخ به این سؤالات هستم که عدم قطعیت واقعاً به چه معنی است؟ آیا همه عدم قطعیت‌ها همانند یکدیگر هستند؟ اگر همه عدم قطعیت‌ها با یکدیگر یکسان نباشند، این چه پیامی برای تصمیم گیران دارد؟

چیزهای زیادی وجود دارد که شما در مورد آن‌ها نامطمئن هستید به دلیل آن‌که اطلاعات یا دانش کافی ندارید. برای مثال ممکن است شما در مورد ارتفاع برج میلاد تهران مطمئن نباشید و یا این‌که رودخانه زاینده‌رود در بهمن‌ماه سال ۱۳۳۰ یخ‌زده بوده است یا نه؛ اما می‌توانید با بررسی مراجع مناسب ارتفاع دقیق برج میلاد را به دست آورید. در مورد دوم شاید مرجع مناسبی پیدا نکنید ولی در هر شکل این سؤالی است که می‌توان با بررسی‌های تاریخی با دقت خوبی پاسخ آن را پیدا کرد. این نوع از عدم قطعیت را عدم قطعیت معرفتی (Epistemic Uncertainty) می‌نامند.

نکته مهم آن است که عدم قطعیت معرفتی قابل کاهش است. با استفاده از ابزارهای اندازه‌گیری دقیق‌تر، به دست آوردن یا خرید اطلاعات و یا سعی و خطا‌های کنترل‌شده می‌توان این نوع از عدم قطعیت‌ را کم کرد.

در حالت دیگر با عدم قطعیتی مواجه هستیم که ناشی از یک فرآیند کاملاً تصادفی (Aleatory Uncertainty) است. یک مثال کلاسیک آن پرتاب سکه و تلاش برای پیش‌بینی نتیجه آن است که شیر یا خط می‌آید. اصطلاحاً گفته می‌شود برآمد شیر یا خط یک متغیر تصادفی (Random Variable) است. این نوع از عدم قطعیت قابل کاهش نیست چراکه ماهیت فرآیند، آن را غیرقابل‌پیش‌بینی می‌کند. در این موارد عمدتاً سعی می‌شود تا عدم قطعیت با تابع توزیع متغیر تصادفی توضیح داده شود. برای مثال اگر فرض کنیم دارای یک سکه منصف هستیم (به این معنی که جرم سکه به‌طور یکسان در آن توزیع شده است و به سمت شیر یا خط متمایل نیست) تابع توزیع متغیر تصادفی آمدن شیر در ۱۰۰ بار پرتاب سکه مانند شکل-۱ است. به‌طور ساده این شکل توضیح می‌دهد از بین این ۱۰۰ بار پرتاب احتمال آنکه n بار شیر بیاید چقدر است. مطابق شکل احتمال آنکه در ۱۰۰ بار پرتاب سکه، نیمی از آن‌ها شیر بیاید چیزی در حدود ۸٫۵ درصد است یا احتمال آنکه همه سکه‌ها شیر بیاید چیزی در حدود صفر یا نامحتمل است.

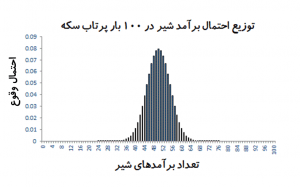
ما می‌توانیم بارها و بارها این آزمایش را تکرار کنیم و هر بار تعداد برآمدهای شیر را بشماریم و به‌این‌ترتیب تابع توزیع آن را مطابق شکل-۱ رسم کنیم، اما این کار تأثیری بر کاهش عدم قطعیت در این فرآیند تصادفی ندارد و تنها کمک ‌می‌کند این عدم قطعیت را بهتر تبیین کنیم.

اما سؤال اینجاست که در دنیای واقعی از کجا متوجه شویم عدم قطعیتی که با آن مواجهیم ناشی از کمبود معرفت است یا ناشی از یک فرآیند کاملاً تصادفی؟

در این خصوص دو رویکرد اصلی وجود دارد. در یک سمت، افرادی هستند که فرآیندهای احتمالی را مبتنی بر فرکانس وقوع توضیح می‌دهند. بسیاری از ما برای اولین بار از این دریچه با مفهوم احتمال آشنا شدیم. مثال پرتاب سکه که در قبل توضیح داده شد دقیقاً مبتنی بر همین رویکرد است. در این حالت شما یک فرایند تصادفی را بارها و بارها تکرار و مشاهده می‌کنید و تابع توزیع احتمال آن را به دست می‌آورید. طبیعی است در این رویکرد باید فرآیند تکرارپذیر باشد تا بتوان تابع توزیع را مشخص کرد.

در سمت دیگر رویکرد بیزی (Bayesian Approach) قرار دارد. از این منظر احتمال یک گزاره به‌سادگی نشان‌دهنده میزان باور شما به صحت آن گزاره است. در اینجا صحبت از گزاره است (عبارتی که یا غلط است یا درست) و نه رویداد (چیزی که می‌تواند رخ دهد یا رخ ندهد). از دیدگاه آمار بیزی احتمال یک مسئله قضاوتی است و بنابراین افراد مختلف می‌توانند دیدگاه متفاوتی نسبت به عدم قطعیت یک گزاره داشته باشند. البته این دیدگاهی است که طرفداران رویکرد اول آن را قبول ندارند و بحث‌های زیادی بین این دو طیف وجود دارد که خارج از چارچوب این مقاله است. از دیدگاه بیزی شما با به دست آوردن اطلاعات جدید، ممکن است در احتمال وقوع یک پدیده تجدیدنظر کنید.

از دیدگاه بیزی تمامی عدم قطعیت‌ها به عدم دانش فرد نسبت به فرآیند برمی‌گردد. برای مثال کِلر (Keller) در مقاله بسیار جالبی بحث می‌کند که حتی پرتاب سکه یک مسئله کاملاً معین (Deterministic) و با علم فیزیک نیوتنی قابل‌حل است. او نشان می‌دهد که چگونه با دانستن سرعت خطی و زاویه‌ای پرتاب، می‌توان برآمد سکه را مشخص کرد و هیچ عدم قطعیتی در این مسئله وجود ندارد!

شاید یک رویکرد میانه این باشد که بگوییم اگر فرد تصمیم‌گیر بتواند با به دست آوردن داده‌های بیشتر، عدم قطعیت را کاهش دهد با عدم قطعیت معرفتی مواجه است و در غیر این صورت با عدم قطعیت ناشی از یک فرآیند کاملاً تصادفی. در این رویکرد دیگر عدم قطعیت نمی‌تواند ذاتی باشد، بلکه به توانایی تصمیم‌گیر در کاهش عدم قطعیت بستگی دارد.

این بحث چه پیامی برای تصمیم‌گیران و مدیران دارد؟

برای مواجهه با ریسک، اهمیت دارد که بدانید با کدام نوع از عدم قطعیت سروکار دارید. اگر با عدم قطعیت معرفتی سروکار دارید، باید تلاش کنید تا کمبود دانش خود را جبران کنید. در حالتی که خود را با یک فرآیند کاملاً تصادفی مواجه می‌دانید، استفاده از داده‌های گذشته و ساختن مدل‌های آماری می‌تواند به شما کمک کند که ارزیابی بهتری از ریسکی که با آن مواجه هستید، داشته باشید.

بسیار مهم است که در گام اول سعی کنید عدم قطعیت را به شکل صریح و روشن بیان کنید. مشاهده می‌کنم بسیاری از افراد برای توصیف عدم قطعیت از واژه‌های مبهم استفاده می‌کنند؛ برای مثال جملاتی مانند “اگر من این سرمایه‌گذاری را انجام دهم، ممکن است ضرر کنم” و یا “اگر شرکت ما این پروژه را از دست بدهد، دچار مشکل شدید مالی می‌شویم.” بیان عدم قطعیت به این شکل تنها نگرانی فرد را افزایش می‌دهد، بدون آن‌که سعی کند دانش جدیدی به او اضافه کند و عمدتاً وی را در موضع انفعالی قرار می‌دهد.

توصیه می‌شود اگر با عدم قطعیت یا ریسک مواجه هستید آن را در قالبی مانند زیر بیان کنید:

اگر “این اتفاقِ همراه با عدم قطعیت” رخ دهد، “این پیامدها” موجب “این اثرات” بر روی “این اهداف” خواهد شد.

به‌عنوان یک مثال ساده:

“اگر فعالیت الف، ب و ج تا انتهای این ماه به پایان نرسد، ما نمی‌توانیم تا آخر فصل پروژه را تکمیل کنیم که موجب می‌شود مبلغ A تومان را به‌موقع از کارفرما دریافت نکنیم و به اهداف مالی سال ۹۵ نرسیم.”

بیان عدم قطعیت به شکل صریح و روشن خودبه‌خود راه را برای برخورد فعالانه‌تر با ریسک فراهم و به شما کمک می‌کند تا شروع کنید اطلاعات و دانش بیشتری از فرآیند جمع کنید، جهت درک کردن برخی از ابعاد ناشناخته فرآیند سعی و خطاهای کنترل‌شده کنید و راه‌حل‌های جدیدی را برای حل مسئله پیشرو طراحی کنید.

در مقاله “ریسک و ندانسته‌های ناشناخته” به این می پردازم که چگونه آن چیزهایی که “نمی‌دانیم” و “نمی‌دانیم که نمی‌دانیم”، ما را در معرض ریسک قرار می‌دهند و چه راه کارهایی برای چنین شرایطی وجود دارد.

منابع:

Keller, J.B. (1986). “The Probability of Heads”, The American Mathematical Monthly, 93 (3), 191-197

O’Hagan, T. (2004). “Dicing with the Unknown”, Significance, 1: 132–۱۳۳

Porter, K. (2016). “Can One Divide Uncertainty into Two Kinds?”, http://www.sparisk.com/pubs/Porter-2016-Two-Kinds-of-Uncertainty.pdf