
دنیای کسبوکار دنیای پیچیدهای است که مدیران باید در فضای آن تصمیمگیری کنند. گرچه پیچیدگی ممکن است برای تصمیمگیران نگرانکننده به نظر برسد، اجتنابی از آن نیست. خبر خوب اینکه دانش بشری در مورد سیستمهای پیچیده (Complex Systems) رو به گسترش بوده است. برای تصمیمگیری بهتر در این فضا، مدیران باید با مفاهیم سیستمهای پیچیده آشنا شوند تا بتوانند به مسائل دنیای کسبوکار بهتر فکر کنند و این مفاهیم را در دنیای واقعی بکار ببرند.
هدف من در این مقاله پرداختن به یکی از ویژگیهای سیستمهای پیچیده است. نحوه تجمیع رفتارهای اجزاء در سیستمهای پیچیده یکی از موضوعات بسیار جالب در این حوزه است. پیشتر در یکی دیگر از مقالاتم به این پرداختم که چگونه ممکن است در سیستمهای پیچیده رفتارهایی که در سطح کلان دیده میشود نتیجه تجمیع رفتارهایی کاملاً متناقض در سطح خرد باشد.
در این مقاله یکی دیگر از پیشفرضها در مورد سیستمهای پیچیده به چالش کشیده میشود؛ اینکه رفتارهای پیچیده لزوماً نتیجه یک طرح و برنامه پیچیده نیست. اجزاء یک سیستم میتوانند تحت یک سری قوانین بسیار ساده با یکدیگر تعامل کنند و از برآیند این تعامل رفتاری پیچیده بروز کند. برای بررسی این مفهوم، من از ماشینهای خودکار سلولی (Cellular Automata) بهره میبرم. ماشینهای خودکار سلولی مدلهای الگوریتمی هستند که با استفاده از یک سری قوانین ساده، محاسباتی را تکرار میکنند. یکی از معروفترین الگوریتمهای ماشینهای خودکار سلولی بازی زندگی (Game of Life) نام دارد که در ادامه به آن خواهم پرداخت.
بازی زندگی
بازی زندگی بهوسیله ریاضیدان انگلیسی جان کانوی (John Horton Conway) ابداع شد. کانوی به مسئلهای که جان فون نیومن (John von Neumann) در دهه ۱۹۴۰ طرح کرده بود علاقهمند شد. نیومن به دنبال این بود تا ماشینی ابداع کند که دارای این توانایی باشد که خودش را بازتولید کند. بازی زندگی یک نمونه ساده از چنین ماشینی است.
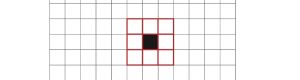
دنیای بازی زندگی شبکهای شطرنجی و نامتناهی از سلولهای مربعی است. هر سلول میتواند زنده یا مرده باشد. در این دنیای دوبعدی هر سلول هشت سلول همسایه دارد (شکل-۱). رفتار هر سلول تنها به وضعیت خودش و هشت سلول مجاور آن بستگی دارد. قوانین زیر بر این دنیا حاکم است:
هر سلول زنده که دارای صفر یا یک همسایه زنده است، خواهد مرد.
هر سلول زنده که دارای دو یا سه همسایه زنده است، به زندگی ادامه خواهد داد.
هر سلول زنده با چهار همسایه یا بیشتر خواهد مرد.
هر سلول مرده که در مجاورت با دقیقاً سه سلول زنده قرار گیرد، زنده خواهد شد.
در هر حالت دیگر، سلول مرده، مرده باقی خواهد ماند.
بازی زندگی با یک ساختار اولیه شروع میشود. به این معنی که در زمان صفر برخی از سلولها مرده و برخی دیگر زنده هستند. با شروع بازی، در هر دور بر اساس قوانین بالا بهطور همزمان وضعیت همه سلولها مشخص میشود و به همین ترتیب دورهای بعدی ادامه مییابد.
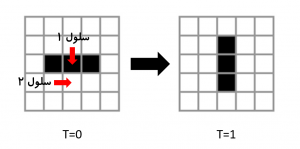
برای مثال فرض کنید در زمان صفر (T=0) وضعیت اولیه دنیای ما مطابق شکل-۲ باشد. سلولهای زنده با رنگ مشکی و سلولهای مرده با رنگ سفید مشخص شدند. به وضعیت سلول ۱ توجه کنید. سلول ۱ زنده و دارای دو همسایه زنده است. مطابق قوانین گفتهشده، در دور بعد نیز زنده میماند. سلول ۲ مرده ولی دارای سه همسایه زنده است. بنابراین سلول ۲ در دور بعد زنده خواهد شد. به همین ترتیب میتوان وضعیت همه سلولها را در دور بعد مشخص کرد و به وضعیت T=1 رسید. در دور بعدی دوباره وضعیت سیستم به حالت اولیه برمیگردد و این الگو به شکل نامحدودی تکرار میشود. این الگو چشمکزن (Blinker) نامگذاری شده است.
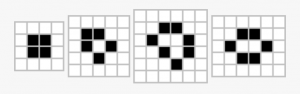
در بازی زندگی، نحوه تعریف شرایط اولیه سیستم رفتار آن را تعیین میکند. مشابه الگوی چشمکزن، شرایط اولیه سیستم را میتوان بهگونهای تعریف کرد که پس از مدتی سیستم به حالت اولیه برگردد. این سیستمها، نوسانگر (Oscillator) نامیده میشوند. برخی از الگوهای معروف نوسانگر در زیر نشان داده شدهاند.




شرایط اولیه سیستم ممکن است بهگونهای تعریف شود که هیچ تغییری در آن به وجود نیاید و سیستم در طول تمام دورهها پایدار بماند. چند نمونه ساده از الگوهای پایدار (Still Life) در شکل-۳ نشان داده شده است.
الگوهای دیگر هم وجود دارند که متحرک هستند. الگوی گلایدر (Glider) یک الگوی تکرارشونده است که پس از چهار دوره، خود را در کمی آنطرفتر تکرار میکند.

از زمان ارائه بازی زندگی در سال ۱۹۷۰ به اینطرف الگوهای زیادی بر اساس همان قوانین ساده کانوی تولید شدهاند. برای مثال الگوی زیر پس از هر دوره مشخص یک گلایدر تولید میکند.
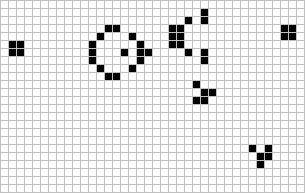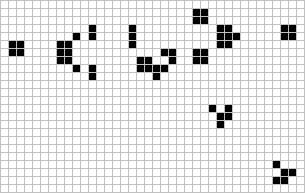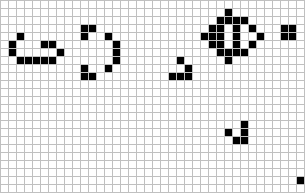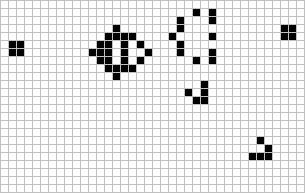
در دنیای بازی زندگی میتوان الگوهایی با رفتارهای بسیار پیچیدهتری را هم دید. برای مثال الگوی زیر قطار دودی (Puffer Train) نام دارد.

حال تصور کنید داستان پشت بازی زندگی را ندانیم و به تصویر بالا نگاه کنیم. از نگاه بیرونی به نظر میرسد موجود یکپارچهای وجود دارد که حرکت میکند، پشت سرخود ردی میگذارد و بهپیش میرود. درحالیکه تنها تعامل سلولها تحت یک سری قوانین ساده چنین الگویی را بروز دادهاند.
با استفاده از نرمافزار موجود در لینک زیر میتوانید شرایط اولیه دلخواه برای سیستم خود تعریف کنید و با کلیک بر روی دکمه Run نتیجه شبیهسازی را ببینید.
نرمافزار شبیهسازی بازی زندگی
ماشینهای خودکار سلولی یکبعدی
کانوی بازی زندگی را در یک دنیای دوبعدی تعریف کرد و عمدتاً توجه را بر روی شرایط اولیه سیستم قرارداد. استیون ولفرام (Stephen Wolfram) بر روی مدل یکبعدی متمرکز شد و بیشتر به بررسی قوانین تعامل سلولها با یکدیگر پرداخت. مشابه بازی زندگی، شرایط هر سلول در دور بعد بر اساس وضعیت خودش و همسایگان مجاور آن تعریف میشود. نمایش حالت یکبعدی با استفاده از شبکهای شطرنجی صورت میگیرد که هر ردیف خروجی هر دوره زمانی را نشان میدهد. ردیف اول از بالا وضعیت سیستم در دور اول و ردیف دوم وضعیت سیستم را در دور دوم نشان میدهد و همینطور ادامه مییابد (شکل-۴).
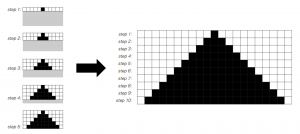
در این مدلسازی ۰ نشاندهنده سلول مرده و ۱ نشاندهنده سلول زنده است. بهاینترتیب برای مثال زنجیره ۱۰۱ نشاندهنده یک سلول مرده است که توسط دو سلول زنده احاطه شده است. فرض کنید وضعیت این سلول در دور بعدی توسط قوانین زیر تعریف میشود:
![]()
برای مثال قانون اول (از سمت چپ) بیان میکند اگر یک سلول زنده دارای دو سلول مجاور زنده باشد، در دور بعد خواهد مرد. قوانین بالا به شکل گرافیکی در شکل-۵ آمدهاند. خروجی باینری این قوانین به شکل ۰۰۰۱۱۱۱۰ است که معادل ۳۰ در سیستم دهدهی است. به همین دلیل به آن قانون ۳۰ (Rule 30) گفته میشود. شکل-۶ بیان گرافیکی یک سیستم را تحت قانون ۳۰ نشان میدهد.


ولفرام در کتاب خود بهصورت مفصل به بررسی قوانین مختلف و الگوهای ناشی از آن میپردازد. شکل-۷ برخی از الگوهایی را که او در کتابش به آن پرداخته نشان میدهد.
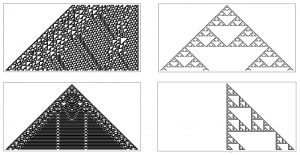
مجدداً آنچه قابلتوجه است بروز الگوهایی پیچیده نشأت گرفته از یک سری قوانین ساده است. اگرچه ما آگاهی کاملی ازآنچه در سطح خرد رخ میدهد داریم، بروز رفتارهای کلان شگفتی ایجاد میکند. به قول ارسطو (Aristotle)، این کل بزرگتر از مجموع اجزاء آن است.
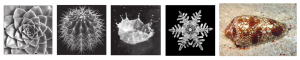
ولفرام در کتاب خود به کاربرد الگوریتمهای ماشینهای خودکار سلولی در حوزههای مختلفی مانند زیستشناسی، مکانیک سیالات، بلورشناسی، فیزیک و رمزنگاری میپردازد و سعی میکند الگوهای مختلف موجود در دنیای واقعی را توضیح دهد (شکل-۸).
ماشینهای خودکار سلولی و بازارهای مالی
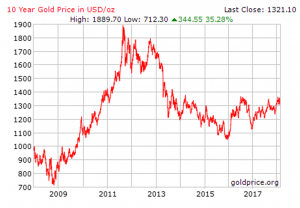
تصادفی بودن (Randomness) قیمتها و نوسانات آن یکی از بارزترین ویژگیهای بازارهای مالی است. به قیمتها در بازارهای مختلف مالی که نگاه کنید یک روند کلی را میبینید اما مقادیر قیمت دارای نوسان حول آن روند هستند. برای مثال شکل-۹ روند تغییرات قیمت هر اونس طلا را برحسب دلار نشان میدهد. منبع این رفتارهای تصادفی چیست؟
در علم اقتصاد قیمت نشاندهنده ارزش یک دارایی است. ارزش یک دارایی منعکسکننده همه عایدیهای آتی آن است. اگر چنین باشد چرا باید در قیمت نوسان وجود داشته باشد؟ اغلب اینطور بیان میشود که در عمل قیمت نه بهوسیله ارزش دارایی بلکه توسط بهترین برآورد از ارزش آن تخمین زده میشود. این برآوردها تحت تأثیر انواع و اقسام اخبار و اتفاقاتی که در سراسر جهان رخ میدهد قرار میگیرد و موجب حرکات تصادفی قیمت میشود. از این منظر وجود نوسانات در قیمت متأثر از نوسانات در محیط بیرون است.
گرچه چنین تفسیری از نوسانات قیمت برای بازه زمانی ماه یا هفته و یا در برخی موارد روز و یا ساعت ممکن است درست به نظر برسد، چه طور این استدلال را برای بازههای زمانی کوچکتر مانند دقیقه یا ثانیه میتوان معتبر دانست. علاوه بر این زمانهایی وجود دارند که در دنیای بیرون اتفاق خاصی نمیافتد ولی قیمتها همچنان دارای بعضاً نوسانهای شدید هستند.
شواهد تجربی نشان میدهد در بازههای زمانی کوتاه نوسانات قیمت بیشتر ناشی از پویایی داخل خود بازار است. اما چطور میتوان این پویایی را توضیح داد؟
در اینجا من برای توضیح این پویایی به مدل بسیار سادهای با استفاده از ماشینهای خودکار سلولی یکبعدی میپردازم. در این مدل هر سلول نشاندهنده یک معاملهگر در بازار است. رنگ هر سلول نشان میدهد که آن معاملهگر میخواهد دارایی را بفروشد یا بخرد. برای قوانین معامله میتوان حالتهای متنوعی را در نظر گرفت ولی در اینجا من به یک حالت ساده که منعکسکننده تأثیرگذاری اطلاعات بازار بر معاملهگر است، اکتفا میکنم. در این مدل هر معاملهگر به همسایههای مجاور خود نگاه میکند و در مورد خرید یا فروش دارایی در دور بعد تصمیم میگیرد. قوانین این مدل در شکل-۱۰ نشان داده شده است.
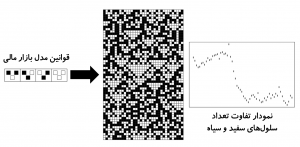
در ابتدا به نظر میرسد چنین مدل سادهای نمیتواند شباهتی به بازارهای مالی در دنیای واقعی داشته باشد و نباید رفتار نوسانی و غیرعادی از خود نشان دهد. در شکل-۱۰ یک نمونه از شبیهسازی چنین بازاری نشان داده شده است. نمودار سمت راست نشاندهنده تفاوت تعداد سلولهای سفید و سیاه در هر دور از شبیهسازی است که منعکسکننده تفاوت عرضه و تقاضاست و بهنوعی قیمت را نمایندگی میکند. همانطور که میبینید این نمودار مشابه نمودارهای قیمت داراییها در بازارهای مالی دارای نوسان است و عامل تصادفی بودن را میتوان در آن مشاهده کرد.
این بحث چه پیامی دارد؟
هدف اصلی من در این مقاله به چالش کشیدن این پیشفرض ذهنی بود که رفتارهای پیچیده در سیستمهای اقتصادی-اجتماعی لزوماً متأثر از قوانین پیچیده نیست. قوانین ساده میتوانند الگوهای رفتاری پیچیدهای ایجاد کنند.
نکته دیگر اینکه همانطور که در بازی زندگی مشاهده کردید و میتوانید در نرمافزار نیز امتحان کنید، قدری تفاوت در شرایط اولیه سیستم میتواند منجر به خروجیهای کاملاً متفاوتی شود.
همانطور که مشاهده شد الگوها و یا رفتارهای پیچیده میتوانند بدون آنکه کسی آن را از قبل طراحی کند، به وجود بیایند. از این مفهوم بهعنوان خودسازماندهی (Self-Organization) یاد میشود. در مثالهای بالا هیچیک از المانهای سیستم و یا فردی از بیرون خروجی سیستم را طراحی نکرده بلکه رفتار جمعی ناشی از بروز و تجمیع رفتارهای اجزاء سیستم است که از قوانین سادهای پیروی میکنند. یک مثال ملموس از خودسازماندهی زبان است. زبان فارسی در طی هزاران سال و ناشی از کنش مردمانی که در فلات ایران زیستهاند بروز و تکامل پیدا است. هیچ طراحی از قبل آن را به وجود نیاورده و مسیر آن را مشخص نکرده است.
در مقاله “چگونه رفتار جمعی یک جامعه میتواند متفاوت از جمع رفتار تکتک افراد آن جامعه باشد؟” به مثال دیگری از نحوه بروز الگوهای کلان بر اساس رفتارهای خرد پرداختم.
منابع:
Adamatzky, A. (2010). “Game of Life Cellular Automata” (Vol. 1). London: Springer
Wolfram, S. (2002). “A New Kind of Science” (Vol. 5). Champaign: Wolfram Media
