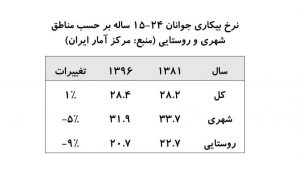
پارادوکس سیمپسون: وقتی واقعیت‌ها، همه واقعیت نیستند

بر اساس اطلاعاتی که اخیراً مرکز آمار ایران منتشر کرده نرخ بیکاری جوانان (طبق تعریف ۱۵ تا ۲۴ ساله) در سال ۱۳۹۶ برای جمعیت شهری ۳۱٫۹ درصد و برای جمعیت روستایی ۲۰٫۷ درصد بوده است. این در حالی است که نرخ بیکاری جوانان در سال ۱۳۸۱ برای جمعیت شهری ۳۳٫۷ درصد و برای جمعیت روستایی ۲۲٫۷ درصد اعلام شده است. به نظر خبر خوبی می‌آید. در طی یک روند بلندمدت نرخ بیکاری جوانان در مناطق شهری ۵ درصد و در مناطق روستایی ۹ درصد کاهش پیدا کرده است.

اما اگر به جدول تهیه‌شده توسط مرکز آمار ایران نگاه کنید (شکل-۱)، آمار بیکاری جوانان برای کل کشور را نیز می‌توانید مشاهده کنید. در کمال تعجب مشاهده می‌شود که نرخ کل بیکاری ۱ درصد افزایش داشته؛ از ۲۸٫۲ درصد به ۲۸٫۴ درصد رسیده است! چطور ممکن است هر دو تصویر درست باشد: نرخ بیکاری در هر دو زیرگروه کاهش داشته، ولی نرخ بیکاری در کل افزایش پیدا کرده است؟

این یک مثال جالب از بروز پارادوکس سیمپسون (Simpson’s Paradox) در داده‌های بازار کار ایران است. پارادوکس سیمپسون زمانی پیش می‌آید که روندی که در سطح گروه‌ها دیده می‌شود، با تجمیع داده‌ها ناپدید و یا کاملاً برعکس می‌شود. در این مقاله با استفاده از مثال‌های مختلف از دنیای واقعی به توضیح پارادوکس سیمپسون و دلالت‌های بروز آن در تصمیم‌گیری می‌پردازم.

پارادوکس سیمپسون و تبعیض جنسیتی

یکی از پر ارجاع‌ترین مقالات در این حوزه، به مقاله‌ای مربوط می‌شود که مسئله تبعیض جنسیتی در دانشگاه کالیفرنیا در برکلی (University of California, Berkeley) را تحلیل و بررسی می‌کند. در سال ۱۹۷۱، از این دانشگاه شکایتی شد مبنی بر اینکه در پذیرش دانشجوی تحصیلات تکمیلی تبعیض جنسیتی بر ضد زنان قائل می‌شود. درصد پذیرش در بین زنان و مردان به نظر تبعیض‌آمیز می‌آمد؛ ۴۴ درصد متقاضیان مرد از این دانشگاه پذیرش گرفته بودند، درحالی‌که این عدد برای زنان ۳۵ درصد بود (شکل-۲).

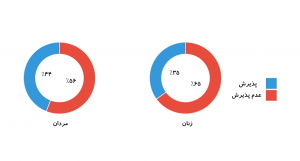
به‌این‌ترتیب به نظر می‌آمد مردان با احتمال بیشتری شانس پذیرش داشتند. وقتی محققان شروع به بررسی شواهد بیشتری کردند، نکته غافلگیرکننده‌ای را متوجه شدند: وقتی داده‌ها در سطح هر دپارتمان تحلیل می‌شد، اثر چنین تبعیضی از بین می‌رفت (شکل-۳). حتی تحلیل‌ها نشان می‌داد ازنظر معنی‌داری آماری کمی سوگیری به سمت زنان وجود داشت.

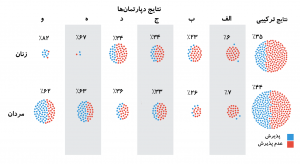
تحلیل در سطح دپارتمان‌ها نشان می‌داد که مردان بیشتر از دپارتمان‌های مهندسی و علوم درخواست پذیرش می‌کنند درحالی‌که زنان بیشتر به رشته‌های علوم انسانی متمایل هستند. برای ورود به رشته‌های مهندسی مهارت‌های تخصصی نیاز است ولی تعداد بیشتری از افراد را پذیرش می‌کنند. درحالی‌که رشته‌های علوم انسانی شرایط ورود راحت‌تری دارند ولی تعداد بسیار کمتری را می‌پذیرند. به‌عبارت‌دیگر تبعیض نه در پذیرش در مقطع کارشناسی ارشد بلکه خیلی قبل از این رخ می‌دهد. نوع انتظارات اجتماع از زنان، زن‌ها را به سمت رشته‌هایی که افراد زیادی در مقطع کارشناسی آن تحصیل می‌کنند، پول کمتری به دانشکده‌هایشان می‌رسد و آینده شغلی مطمئنی ندارند سوق می‌دهد.

پارادوکس سیمپسون (Simpson’s Paradox) در حالتی می‌تواند رخ دهد که حداقل سه متغیر در مسئله درگیر باشند: متغیری که توضیح داده می‌شود (یا متغیر وابسته)، متغیری که توضیح‌دهنده است و متغیر سومی که اگرچه مؤثر است، اثر آن مورد غفلت واقع می‌شود. پارادوکس سیمپسون زمانی حاصل می‌شود که اثر متغیر توضیح‌دهنده بر روی متغیر وابسته با در نظر گرفتن متغیر سوم برعکس می‌شود. این پدیده وقتی ادوارد سیمپسون (Edward H. Simpson) در مقاله خود در سال ۱۹۵۱ به آن اشاره کرد، موردتوجه قرار گرفت. گرچه پیش از او نیز آماردانان دیگری به آن اشاره کرده بودند.

توجه کنید این‌ها شرط لازم هستند نه کافی. خوانندگان علاقه‌مند به بحث‌های فنی‌تر می‌توانند بخش ضمیمه این مقاله را مطالعه کنند.

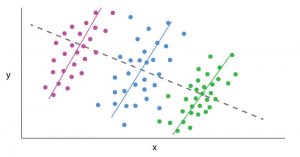
برای مثال در شکل-۴ با نگاه کردن به همه داده‌ها و خط خاکستری‌رنگ به نظر می‌رسد اثر x (متغیر توضیح‌دهنده) بر روی y (متغیر وابسته) منفی است. اما وقتی رنگ‌های بنفش، آبی و سبز را در نظر بگیریم (متغیر سوم)، متغیر توضیح‌دهنده یا x اثر مثبتی بر روی y می‌گذارد.

چرا پارادوکس سیمپسون مهم است؟

همان‌طور که در مثال‌های بالا دیده می‌شود، در صورت بروز پارادوکس سیمپسون در داده‌ها، تصویر دوگانه‌ای پیش روی تصمیم‌گیر قرار می‌گیرد. یک مثال واقعی مربوط به یک مطالعه پزشکی برای سنجش میزان موفقیت دو روش درمان سنگ کلیه بوده است. شکل-۵ تعداد کل درمان‌ها و نرخ موفقیت هر دو روش را در درمان‌های پزشکی انجام‌شده نشان می‌دهد. این‌طور به نظر می‌رسد روش درمانی الف چه بر روی سنگ کلیه‌های کوچک و چه بزرگ نرخ موفقیت بالایی را نسبت به روش ب داشته است. اما وقتی به نتایج ترکیبی آزمایش‌ها نگاه می‌کنیم، روش درمانی ب نرخ موفقیت بالاتری دارد. کدام تصویر درست است؟

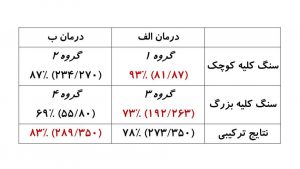
مهم‌تر این‌که در تصمیم‌گیری درباره درمان، کدام تصویر باید ملاک عمل قرار گیرد؟ اگر کسی دارای سنگ کلیه بزرگ یا کوچک باشد، روش الف برتر از روش ب است. اما اگر ندانیم اندازه سنگ کلیه چقدر است، چه تصمیمی باید گرفت؟ آیا باید روش ب را توصیه کرد که در کل نرخ موفقیت بالاتری دارد؟ این نتیجه‌گیری عجیب به نظر می‌رسد. چون وقتی یک تصمیم در دو حالت ممکن بهینه است، اگر ندانیم در کدام‌یک از این دو حالت به سر می‌بریم، بازهم باید آن تصمیم بهینه باشد.

برای پاسخ به این پرسش باید مسئله را عمیق‌تر بررسی کرد. در اینجا یک متغیر سوم، وخامت بیماری، که تا پیش از آن در نظر گرفته نشده بود، اهمیت می‌یابد. پزشکان برای موارد بدخیم‌تر (سنگ‌های کلیه بزرگ‌تر) روش درمانی الف را که بهتر می‌دانستند، انجام می‌دادند. درحالی‌که برای موارد خوش‌خیم‌تر (سنگ‌های کلیه کوچک) پزشکان روش درمانی ضعیف‌تر (روش ب) را اجرا می‌کردند. درنتیجه در جدول می‌بینید که نمونه‌های آماری در گروه‌های دوم و سوم بسیار بزرگ‌تر از گروه‌های اول و سوم است. به‌این‌ترتیب نتایج درمانی در گروه‌های دوم و چهارم در ارزیابی کلی پررنگ می‌شود. اما چون موارد بدخیم که نوعاً شانس درمان موفقیت‌آمیز کمتری دارند با روش الف درمان می‌شوند، روش الف در کل ضعیف‌تر نشان داده می‌شود.

پس نتایج به‌ظاهر متناقض در اثر در نظر نگرفتن اثر متغیر سوم که میزان وخامت بیماری است، ظاهر می‌شود. درواقع جمع‌بندی نهایی این است که وقتی روش ناکارآمدتر بیشتر در موارد خوش‌خیم بکار می‌رود، در کل به نظر مؤثرتر می‌رسد.

در مثال داده‌های بازار کار در ایران، باید توجه کنیم تغییرات بنیادی بین سال‌های ۱۳۸۱ تا ۱۳۹۶ در جمعیت ایران رخ داده است. جمعیت شهری رشدی ۳۵ درصدی تجربه کرده درحالی‌که جمعیت روستایی رشد منفی ۸ درصدی داشته است. در سال ۱۳۹۵ جمعیت شهری حدود ۲٫۸۵ برابر جمعیت روستایی بوده است. بنابراین نرخ بیکاری جوانان شهری خود را بیشتر و بیشتر در نرخ بیکاری کل بازتاب می‌دهد.

توضیح بیشتر آن‌که در سال ۱۳۸۱ نرخ بیکاری شهری و روستایی به ترتیب ۳۳٫۷ و ۲۲٫۷ درصد است. نرخ بیکاری کل که درواقع میانگین وزنی این دو عدد است، باید چیزی بین این دو دربیاید (۲۸٫۲ درصد). در سال ۱۳۹۶ هم نرخ بیکاری کل میانگین وزنی ۳۱٫۹ و ۲۰٫۷ درصد است. ولی چون سهم نرخ بیکاری شهری به خاطر افزایش جمعیت قابل‌توجه بخش شهری زیاد شده، این میانگین وزنی بیشتر و بیشتر به ۳۱٫۹ نزدیک و معادل ۲۸٫۴ شده است.

اهمیت پارادوکس سیمپسون در مدیریت کسب‌وکار

آگاهی تصمیم‌گیر از امکان بروز پارادوکس سیمپسون وقتی وی به دنبال ارزیابی عملکرد گزینه‌هاست اهمیت پیدا می‌کند. شناسایی پارادوکس سیمپسون درحالی‌که شما هم به داده‌های کلان و هم داده‌های زیرگروه‌ها دسترسی دارید، نسبتاً آسان است. با مثال‌هایی که در این مقاله آوردم، احتمالاً بتوانید دلایل ممکن برای بروز این پدیده را در داده‌های خود بررسی کنید.

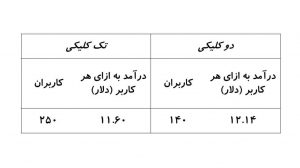
ولی پارادوکس سیمپسون وقتی اهمیت بیشتری پیدا می‌کند که شما بنا به هر دلیلی تصویر کاملی از مسئله نداشته باشید. سال ۲۰۱۰ یک شرکت آمریکایی فعال در حوزه بازاریابی دیجیتال داده‌های مربوط به دو روش متفاوت ارائه تبلیغات را بررسی می‌کرد. در روش اول کاربر با دیدن بنر تبلیغاتی، یک کلیک کرده و به وب‌سایت موردنظر هدایت می‌شد. در روش دوم، کاربر با دیدن بنر ابتدا به یک صفحه میانی که در آن کلیدواژه‌های مختلف و مربوط به تبلیغ بودند هدایت و اگر بر روی یکی از کلیدواژه‌ها کلیک می‌کرد به صفحه نهایی هدایت می‌شد. گرچه مخاطب در روش دو کلیکی باید تلاش بیشتری به خرج می‌داد و بنابراین نرخ تبدیل (نسبت کسانی که روی تبلیغ کلیک می‌کنند به کسانی که آن را می‌بینند) کمتری داشت، ولی انتظار می‌رفت کیفیت کاربرانی که به صفحه نهایی هدایت می‌شوند و درنتیجه درآمد به ازای هر کاربر افزایش یابد.

این شرکت نتایج آزمون A/B را برای این دو روش بررسی کرد. نتایج در شکل-۶ آمده است. نتایج آزمون A/B نشان می‌دهد درآمد به ازای هر کاربر درروش دو کلیکی بالاتر از روش تک کلیکی است. این نتیجه‌گیری می‌توانست تبدیل به خطای گران‌قیمتی برای آن شرکت شود.

یک دانشمند داده در آن شرکت تصمیم می‌گیرد، داده‌ها را بر اساس این‌که کاربران در داخل آمریکا یا خارج آمریکا هستند، برش بزند. نتایج این تحلیل در شکل-۷ نشان داده شده است. همان‌طور که می‌بینید روش تک کلیکی برای کاربران داخل و خارج آمریکا بهتر است. ولی اگر در کل به داده‌ها نگاه کنیم روش دو کلیکی برتر است.

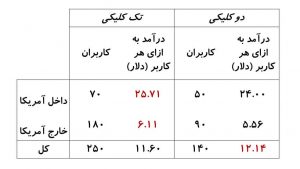
در این مسئله این‌که کاربر از داخل یا خارج آمریکا باشد، نقش متغیر سوم را بازی می‌کند. کارایی روش تبلیغاتی نه‌تنها تابع نوع روش بلکه تابع نوع کاربر نیز هست. کاربران داخل آمریکا نوعاً درآمد سرانه بیشتری نسبت به کاربران خارج آمریکا برای شرکت ایجاد می‌کنند. همین‌طور آنان با احتمال بیشتری تبلیغات دو کلیکی را دنبال می‌کنند. این باعث می‌شود کارایی روش دو کلیکی بیشتر متأثر از رفتار کاربران آمریکایی شود.

برخلاف نتیجه‌گیری اولیه، روش تک کلیکی مؤثرتر از روش دیگر است. اگر شرکت به این نکته توجه نمی‌کرد، نزدیک به یک میلیون دلار از درآمد بالقوه خود را می‌توانست از دست بدهد.

این نمونه‌ها دوباره اهمیت تشخیص درست روابط علت و معلولی را در مدیریت کسب‌وکار یادآوری می‌کنند. یک مدیر توانمند و باهوش بلافاصله با دیدن اطلاعات اولیه، حتی اگر تأییدکننده نظرش باشد، نتیجه‌گیری نمی‌کند. او همواره این احتمال را در نظر دارد که عواملی که خارج از دید هستند، ممکن است نتایج را مخدوش کنند. او می‌داند واقعیت‌هایی که می‌بیند، ممکن است همه واقعیت نباشند.

اگر از خواندن این مقاله لذت بردید، ممکن است مقاله “چرا مدیران باید تفاوت بین همبستگی و رابطه علّی را بدانند؟” برایتان جالب باشد.

***ضمیمه مقاله: فرمول‌بندی ریاضی پارادوکس سیمپسون

در اینجا برای نشان دادن شرایط بروز پارادوکس سیمپسون به مثال تبعیض جنسیتی برمی‌گردم. فرض کنید دو دپارتمان در دانشگاه وجود دارد و ما داده‌های هر دپارتمان و نتایج کلی را برای زنان (F) و مردان (M) در جدول زیر خلاصه کردیم (شکل-۸).

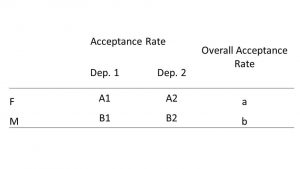
برای چنین جدولی تنها و تنها اگر همه شرایط زیر برقرار باشد، پارادوکس سیمپسون وجود خواهد داشت:

$A1\geq B1$

$A2\geq B2$

$b\geq a$

$(A1-B1)+(A2-B2)+(b-a)>0$

توجه کنید که شرط آخر اهمیت دارد. حالت محتمل زیر را در نظر بگیرید که سه شرط اول در آن برقرار است:

$A1=B1, A2=B2,b=a$

ولی در این حالت پارادوکس سیمپسون برقرار نیست.

محققان نشان دادند، اگر اعداد به شکل تصادفی با توزیع یکنواخت در جدول بالا تولید شوند، احتمال وقوع پارادوکس سیمپسون بین ۱ تا ۲ درصد است.

حالتی که در این مقاله بحث شد، حالت خاصی بود که متغیر توضیح‌دهنده از نوع رسته‌ای (Categorical) است. برای مثال جنسیت تنها دو حالت به خود می‌گیرد. در حالت کلی‌تر که همه متغیرها به‌صورت پیوسته هستند، فرمول‌بندی ریاضی پارادوکس سیمپسون به شکل زیر است.

اگر $X$ و $Z$ دو متغیر تصادفی باشند و فرض شده باشد $X$ عامل $Z$ است، چنین رابطه‌ای بین آن دو برقرار است:

$Z = r_{{ZX}}X+\epsilon$

در رابطه بالا $r_{{ZX}}$ ضریب همبستگی بین دو متغیر و $\epsilon$ مقدار خطایی است که نشان می‌دهد چقدر از واریانس $Z$ نمی‌تواند توسط $X$ توضیح داده شود.

فرض کنید $Y$ یک متغیر تصادفی دیگر است که با $X$ همبستگی دارد و بر روی $Z$ هم اثر مستقیم می‌گذارد. رابطه بین $Z$ و $X$ و $Y$ به شکل زیر صورت‌بندی می‌شود: $Z = p_{{ZX}}X+p_{{ZY}}Y+\theta$

در رابطه بالا $p_{{ZX}}$ ضریب همبستگی بین $Z$ و $X$ ، $p_{{ZY}}$ ضریب همبستگی بین $Z$ و $Y$ و $\theta$ مقدار خطایی است که نشان می‌دهد چقدر از واریانس $Z$ نمی‌تواند توسط $X$ و $Y$ به‌طور مشترک توضیح داده شود.

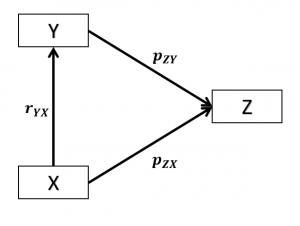
دیاگرام مسیر (Path Diagram) رابطه بین این سه متغیر در شکل-۹ نشان داده شده است. پارادوکس سیمپسون در رابطه بین $X$ و $Z$ وقتی برقرار است که داشته باشیم:

$r_{{ZX}}\times p_{{ZX}}<0$

به همین ترتیب می‌توان شرایط تحقق پارادوکس سیمپسون را برای رابطه $Y$ و $Z$ تعریف کرد ( $r_{{ZY}}\times p_{{ZY}}<0$ ).

نتایج شبیه‌سازی نشان می‌دهد احتمال وقوع پارادوکس سیمپسون برای چنین حالتی حدود ۱۲٫۸ درصد است. این به محققان یادآوری می‌کند که در مطالعات تجربی باید نگران وقوع پارادوکس سیمپسون باشند.

منابع:

درگاه ملی آمار ایران، داده‌های جمعیت و نیروی کار، به نشانی https://www.amar.org.ir/

Bandyoapdhyay, P. S., Nelson, D., Greenwood, M., Brittan, G., & Berwald, J. (2011). “The Logic of Simpson’s paradox” Synthese, 181(2), 185-208

Bickel, P. J., Hammel, E. A., & O’Connell, J. W. (1975). “Sex Bias in Graduate Admissions: Data from Berkeley”. Science, 187(4175), 398-404

Charig, C. R., Webb, D. R., Payne, S. R., & Wickham, J. E. (1986). “Comparison of Treatment of Renal Calculi by Open Surgery, Percutaneous Nephrolithotomy, and Extracorporeal Shockwave Lithotripsy”. Br Med J (Clin Res Ed), 292(6524), 879-882

Kock, N. (2015). “How likely is Simpson’s Paradox in Path Models?” International Journal of e-Collaboration (IJeC), 11(1), 1-7

Ma, Y. Z. (2015). “Simpson’s Paradox in GDP and Per Capita GDP Growths”. Empirical Economics, 49(4), 1301-1315

Smith, G. (2014). “Standard Deviations: Flawed Assumptions, Tortured Data, and Other Ways to Lie with Statistics”, Overlook Duckworth, Peter Mayer Publishers, Inc. New York

4 نظر در “پارادوکس سیمپسون: وقتی واقعیت‌ها، همه واقعیت نیستند”

مهدی
مرداد ۱, ۱۴۰۰ در ۹:۰۲ ب٫ظ
پیوند یکتا
سلام قربان
من شرمندتون شدم، اخرش نفهمیدم چرا نرخ بیکاری (مثال اول) اخرش اونجوری شد؟
پاسخ
- فرزاد مینویینویسنده مطلب
  مرداد ۲, ۱۴۰۰ در ۸:۴۷ ق٫ظ
  پیوند یکتا
  با سلام و وقت بخیر و شادی،
  در این مثال دیدن تصویر کلی بدون درنظر گرفتن تغییرات نرخ بیکاری در شهر و روستا صحیح نیست. چراکه در این بازه تغییرات بنیادی در جمعیت ایران رخ داده است. جمعیت شهری رشد مثبت قابل توجه داشته درحالی‌که جمعیت روستایی رشد منفی داشته است. بنابراین در طول زمان نرخ بیکاری جوانان شهری خود را بیشتر و بیشتر در نرخ بیکاری کل بازتاب می‌دهد.
  در سال ۱۳۸۱ نرخ بیکاری شهری و روستایی به ترتیب ۳۳٫۷ و ۲۲٫۷ درصد است. نرخ بیکاری کل که درواقع میانگین وزنی این دو عدد است، باید چیزی بین این دو دربیاید (۲۸٫۲ درصد). در سال ۱۳۹۶ هم نرخ بیکاری کل میانگین وزنی ۳۱٫۹ و ۲۰٫۷ درصد است. ولی چون سهم نرخ بیکاری شهری به خاطر افزایش جمعیت قابل‌توجه بخش شهری زیاد شده، این میانگین وزنی بیشتر و بیشتر به ۳۱٫۹ نزدیک و معادل ۲۸٫۴ شده است.
  پاسخ
مهدی
آبان ۲۶, ۱۴۰۰ در ۸:۵۹ ب٫ظ
پیوند یکتا
سلام استاد
آخر مقاله که فرموله کردین تفاوت بین r(xz) و P(xz) رو نفهمیدم؟ مگه هر دو تاش ضریب همبستگی بین x و z نیست. و حاصل ضرب این دو تا باید منفی باشه تا پارادوکس سیمپسون رو داشته باشیم؟
لطف میکنید یکم توضیح بدید.
ممنونم
پاسخ
- فرزاد مینویینویسنده مطلب
  آذر ۸, ۱۴۰۰ در ۵:۵۶ ب٫ظ
  پیوند یکتا
  سلام و وقت بخیر
  توجه کنید در توضیح بالا، وقتی تنها رابطه Z و X بررسی می شود از r(zx) برای نمایش همبستگی بین Z و X استفاده کردم. وقتی رابطه Z و X در حضور Y بررسی می شود از p(zx) برای نمایش همبستگی بین Z و X استفاده کردم.
  پاسخ

آنالیکا